Lsh-sampling Breaks the Computation Chicken-and-egg Loop in Adaptive Stochastic Gradient Estimation
Paper and Code
Oct 30, 2019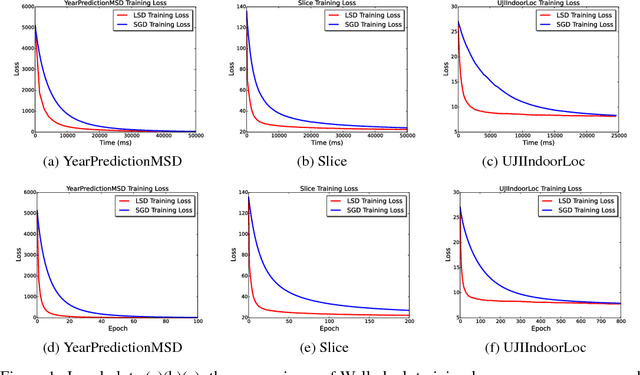
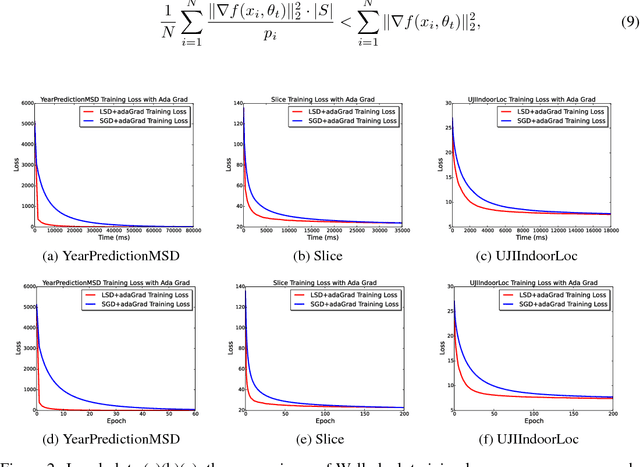
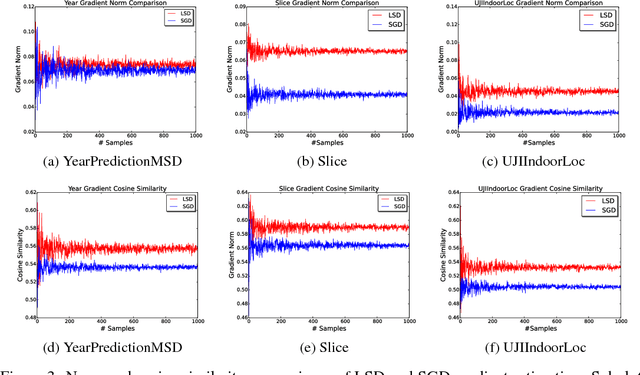
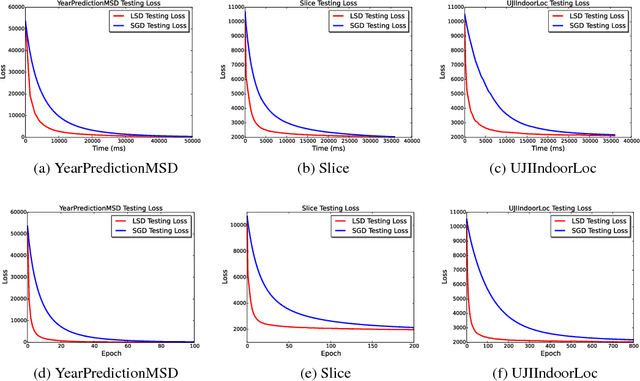
Stochastic Gradient Descent or SGD is the most popular optimization algorithm for large-scale problems. SGD estimates the gradient by uniform sampling with sample size one. There have been several other works that suggest faster epoch-wise convergence by using weighted non-uniform sampling for better gradient estimates. Unfortunately, the per-iteration cost of maintaining this adaptive distribution for gradient estimation is more than calculating the full gradient itself, which we call the chicken-and-the-egg loop. As a result, the false impression of faster convergence in iterations, in reality, leads to slower convergence in time. In this paper, we break this barrier by providing the first demonstration of a scheme, Locality sensitive hashing (LSH) sampled Stochastic Gradient Descent (LGD), which leads to superior gradient estimation while keeping the sampling cost per iteration similar to that of the uniform sampling. Such an algorithm is possible due to the sampling view of LSH, which came to light recently. As a consequence of superior and fast estimation, we reduce the running time of all existing gradient descent algorithms, that relies on gradient estimates including Adam, Ada-grad, etc. We demonstrate the effectiveness of our proposal with experiments on linear models as well as the non-linear BERT, which is a recent popular deep learning based language representation model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge