LS-Net: Learning to Solve Nonlinear Least Squares for Monocular Stereo
Paper and Code
Sep 09, 2018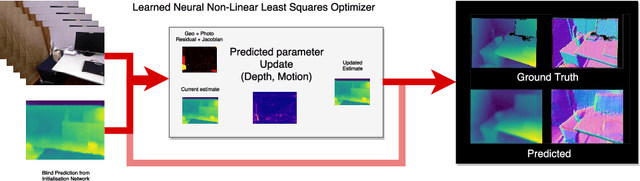
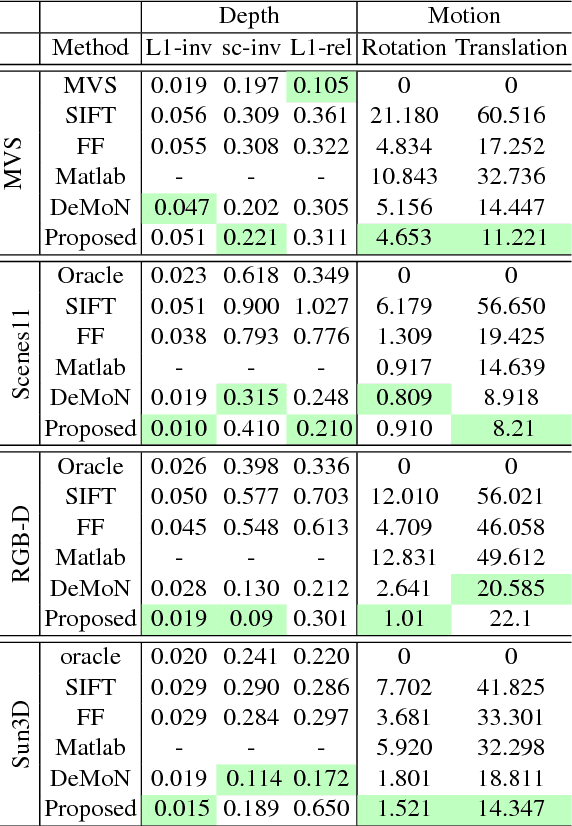
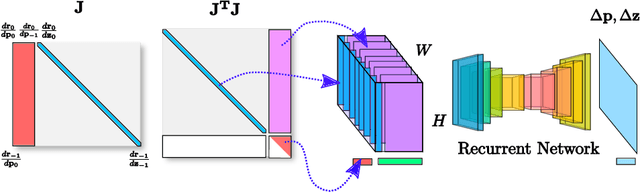
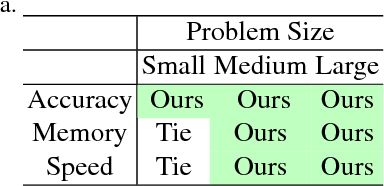
Sum-of-squares objective functions are very popular in computer vision algorithms. However, these objective functions are not always easy to optimize. The underlying assumptions made by solvers are often not satisfied and many problems are inherently ill-posed. In this paper, we propose LS-Net, a neural nonlinear least squares optimization algorithm which learns to effectively optimize these cost functions even in the presence of adversities. Unlike traditional approaches, the proposed solver requires no hand-crafted regularizers or priors as these are implicitly learned from the data. We apply our method to the problem of motion stereo ie. jointly estimating the motion and scene geometry from pairs of images of a monocular sequence. We show that our learned optimizer is able to efficiently and effectively solve this challenging optimization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge