Low-Rank Matrix Recovery with Scaled Subgradient Methods: Fast and Robust Convergence Without the Condition Number
Paper and Code
Oct 26, 2020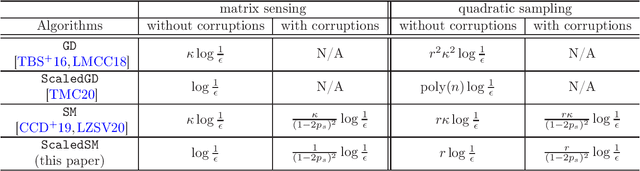
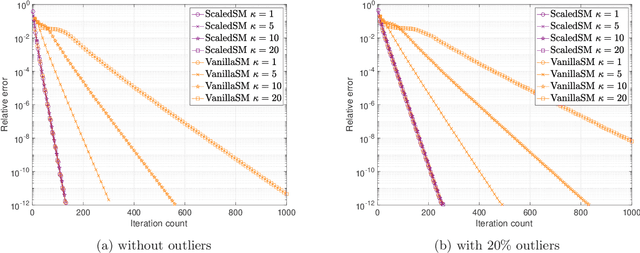
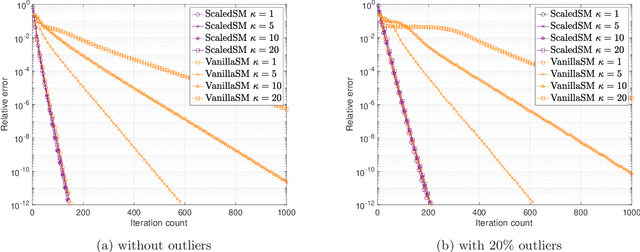
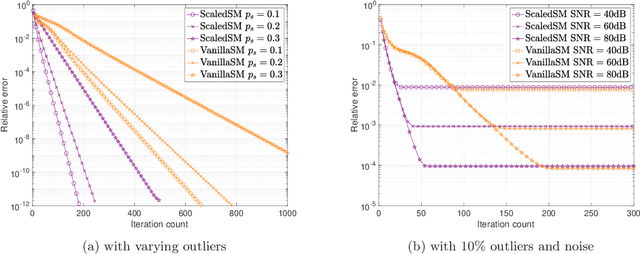
Many problems in data science can be treated as estimating a low-rank matrix from highly incomplete, sometimes even corrupted, observations. One popular approach is to resort to matrix factorization, where the low-rank matrix factors are optimized via first-order methods over a smooth loss function, such as the residual sum of squares. While tremendous progresses have been made in recent years, the natural smooth formulation suffers from two sources of ill-conditioning, where the iteration complexity of gradient descent scales poorly both with the dimension as well as the condition number of the low-rank matrix. Moreover, the smooth formulation is not robust to corruptions. In this paper, we propose scaled subgradient methods to minimize a family of nonsmooth and nonconvex formulations -- in particular, the residual sum of absolute errors -- which is guaranteed to converge at a fast rate that is almost dimension-free and independent of the condition number, even in the presence of corruptions. We illustrate the effectiveness of our approach when the observation operator satisfies certain mixed-norm restricted isometry properties, and derive state-of-the-art performance guarantees for a variety of problems such as robust low-rank matrix sensing and quadratic sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge