Low-Precision Random Fourier Features for Memory-Constrained Kernel Approximation

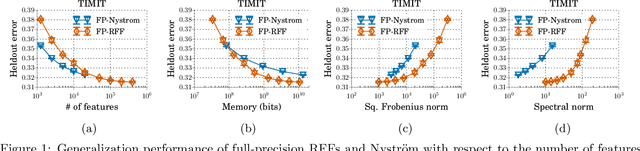
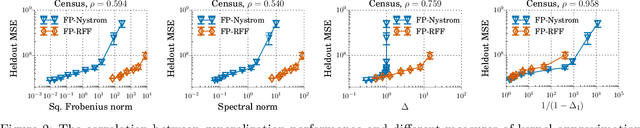
We investigate how to train kernel approximation methods that generalize well under a memory budget. Building on recent theoretical work, we define a measure of kernel approximation error which we find to be much more predictive of the empirical generalization performance of kernel approximation methods than conventional metrics. An important consequence of this definition is that a kernel approximation matrix must be high-rank to attain close approximation. Because storing a high-rank approximation is memory-intensive, we propose using a low-precision quantization of random Fourier features (LP-RFFs) to build a high-rank approximation under a memory budget. Theoretically, we show quantization has a negligible effect on generalization performance in important settings. Empirically, we demonstrate across four benchmark datasets that LP-RFFs can match the performance of full-precision RFFs and the Nystr\"{o}m method, with 3x-10x and 50x-460x less memory, respectively.