Local vs. Global Interpretability: A Computational Complexity Perspective
Paper and Code
Jun 07, 2024
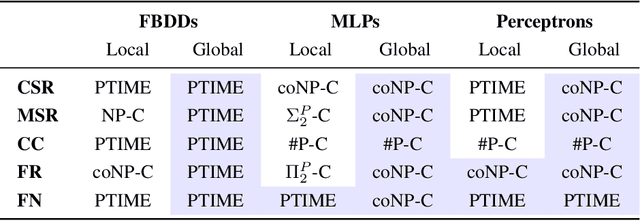
The local and global interpretability of various ML models has been studied extensively in recent years. However, despite significant progress in the field, many known results remain informal or lack sufficient mathematical rigor. We propose a framework for bridging this gap, by using computational complexity theory to assess local and global perspectives of interpreting ML models. We begin by proposing proofs for two novel insights that are essential for our analysis: (1) a duality between local and global forms of explanations; and (2) the inherent uniqueness of certain global explanation forms. We then use these insights to evaluate the complexity of computing explanations, across three model types representing the extremes of the interpretability spectrum: (1) linear models; (2) decision trees; and (3) neural networks. Our findings offer insights into both the local and global interpretability of these models. For instance, under standard complexity assumptions such as P != NP, we prove that selecting global sufficient subsets in linear models is computationally harder than selecting local subsets. Interestingly, with neural networks and decision trees, the opposite is true: it is harder to carry out this task locally than globally. We believe that our findings demonstrate how examining explainability through a computational complexity lens can help us develop a more rigorous grasp of the inherent interpretability of ML models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge