Lipschitz-bounded 1D convolutional neural networks using the Cayley transform and the controllability Gramian

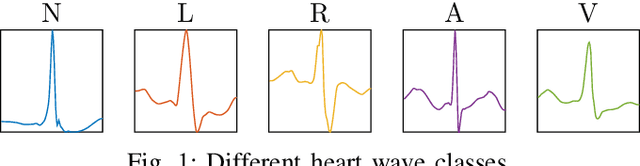
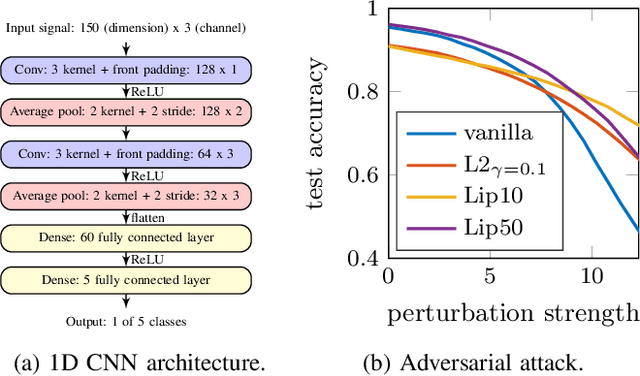
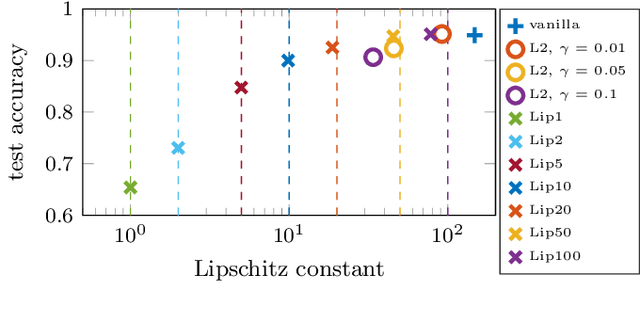
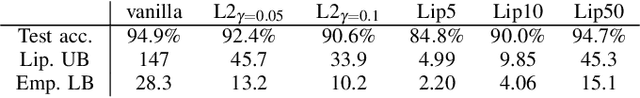
We establish a layer-wise parameterization for 1D convolutional neural networks (CNNs) with built-in end-to-end robustness guarantees. Herein, we use the Lipschitz constant of the input-output mapping characterized by a CNN as a robustness measure. We base our parameterization on the Cayley transform that parameterizes orthogonal matrices and the controllability Gramian for the state space representation of the convolutional layers. The proposed parameterization by design fulfills linear matrix inequalities that are sufficient for Lipschitz continuity of the CNN, which further enables unconstrained training of Lipschitz-bounded 1D CNNs. Finally, we train Lipschitz-bounded 1D CNNs for the classification of heart arrythmia data and show their improved robustness.