Link Prediction with Attention Applied on Multiple Knowledge Graph Embedding Models
Paper and Code
Feb 13, 2023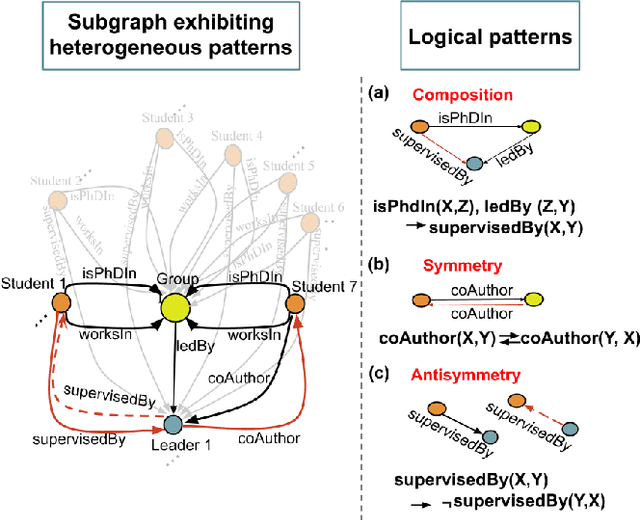

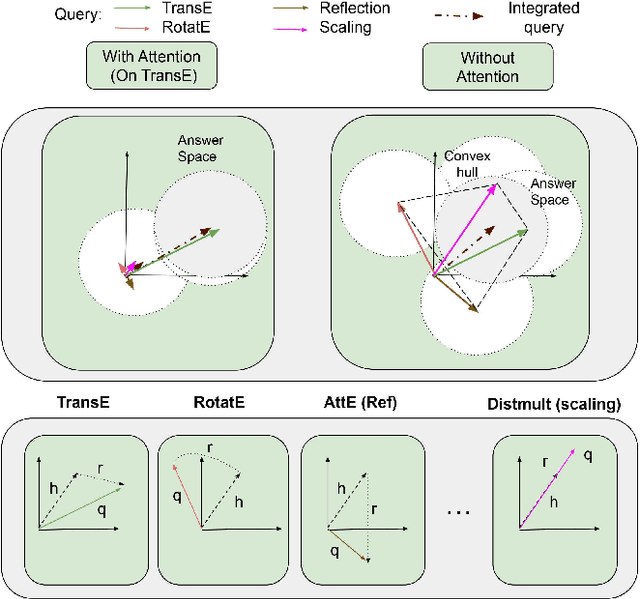
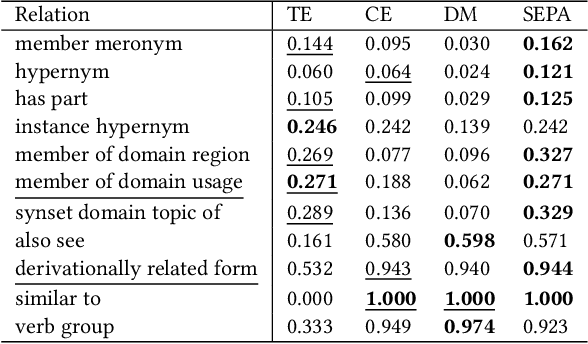
Predicting missing links between entities in a knowledge graph is a fundamental task to deal with the incompleteness of data on the Web. Knowledge graph embeddings map nodes into a vector space to predict new links, scoring them according to geometric criteria. Relations in the graph may follow patterns that can be learned, e.g., some relations might be symmetric and others might be hierarchical. However, the learning capability of different embedding models varies for each pattern and, so far, no single model can learn all patterns equally well. In this paper, we combine the query representations from several models in a unified one to incorporate patterns that are independently captured by each model. Our combination uses attention to select the most suitable model to answer each query. The models are also mapped onto a non-Euclidean manifold, the Poincar\'e ball, to capture structural patterns, such as hierarchies, besides relational patterns, such as symmetry. We prove that our combination provides a higher expressiveness and inference power than each model on its own. As a result, the combined model can learn relational and structural patterns. We conduct extensive experimental analysis with various link prediction benchmarks showing that the combined model outperforms individual models, including state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge