Linear Coding for Gaussian Two-Way Channels
Paper and Code
Oct 29, 2022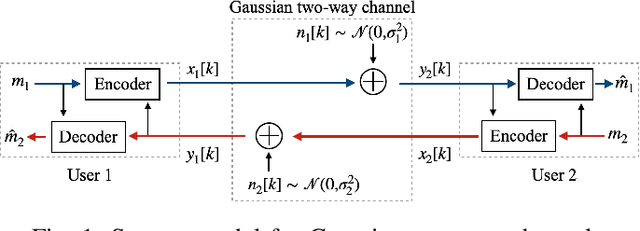
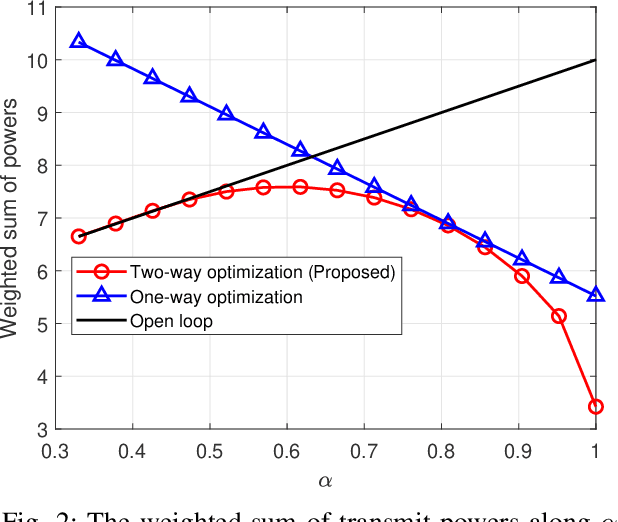
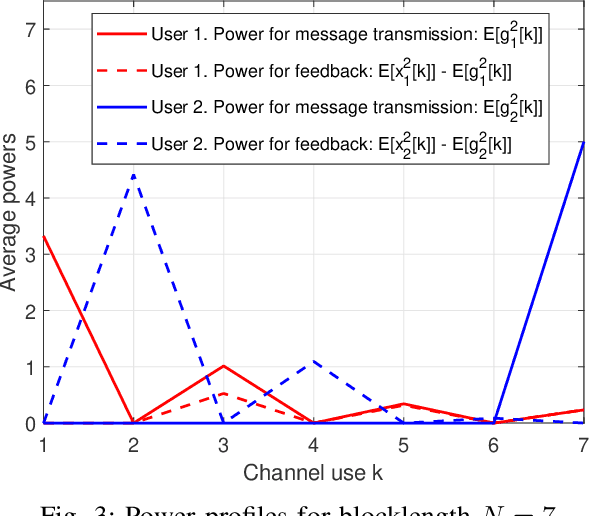

We consider linear coding for Gaussian two-way channels (GTWCs), in which each user generates the transmit symbols by linearly encoding both its message and the past received symbols (i.e., the feedback information) from the other user. In Gaussian one-way channels (GOWCs), Butman has proposed a well-developed model for linear encoding that encapsulates feedback information into transmit signals. However, such a model for GTWCs has not been well studied since the coupling of the encoding processes at the users in GTWCs renders the encoding design non-trivial and challenging. In this paper, we aim to fill this gap in the literature by extending the existing signal models in GOWCs to GTWCs. With our developed signal model for GTWCs, we formulate an optimization problem to jointly design the encoding/decoding schemes for both the users, aiming to minimize the weighted sum of their transmit powers under signal-to-noise ratio constraints. First, we derive an optimal form of the linear decoding schemes under any arbitrary encoding schemes employed at the users. Further, we provide new insights on the encoding design for GTWCs. In particular, we show that it is optimal that one of the users (i) does not transmit the feedback information to the other user at the last channel use, and (ii) transmits its message only over the last channel use. With these solution behaviors, we further simplify the problem and solve it via an iterative two-way optimization scheme. We numerically demonstrate that our proposed scheme for GTWCs achieves a better performance in terms of the transmit power compared to the existing counterparts, such as the non-feedback scheme and one-way optimization scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge