Linear Bandits with Feature Feedback
Paper and Code
Mar 12, 2019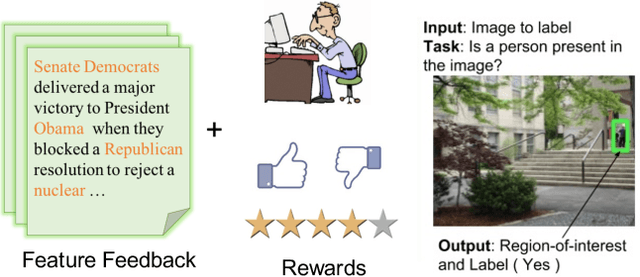
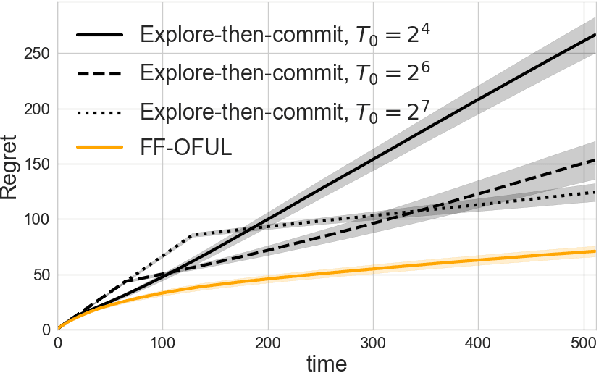

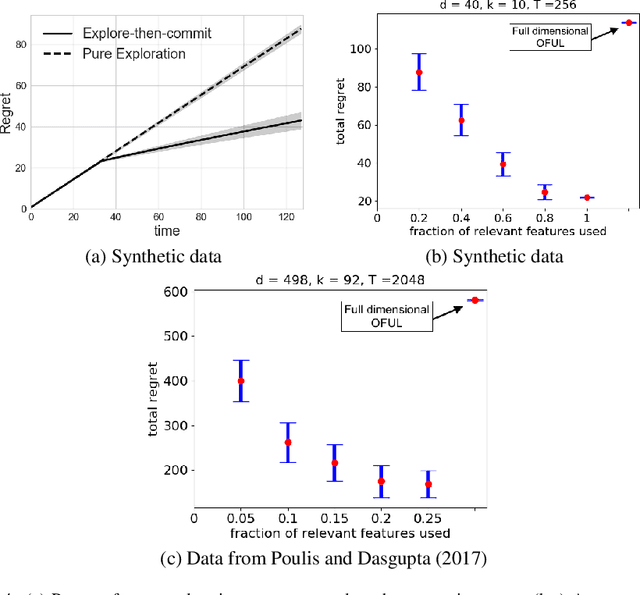
This paper explores a new form of the linear bandit problem in which the algorithm receives the usual stochastic rewards as well as stochastic feedback about which features are relevant to the rewards, the latter feedback being the novel aspect. The focus of this paper is the development of new theory and algorithms for linear bandits with feature feedback. We show that linear bandits with feature feedback can achieve regret over time horizon $T$ that scales like $k\sqrt{T}$, without prior knowledge of which features are relevant nor the number $k$ of relevant features. In comparison, the regret of traditional linear bandits is $d\sqrt{T}$, where $d$ is the total number of (relevant and irrelevant) features, so the improvement can be dramatic if $k\ll d$. The computational complexity of the new algorithm is proportional to $k$ rather than $d$, making it much more suitable for real-world applications compared to traditional linear bandits. We demonstrate the performance of the new algorithm with synthetic and real human-labeled data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge