Limiting Spectrum of Randomized Hadamard Transform and Optimal Iterative Sketching Methods

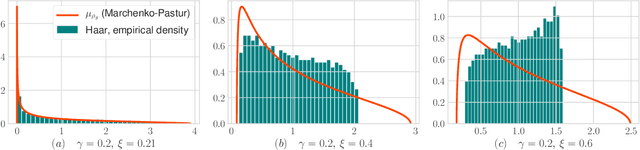
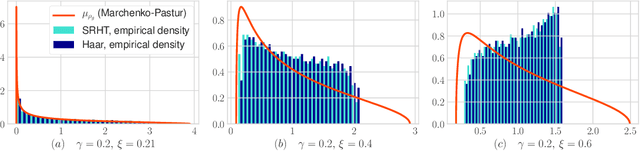
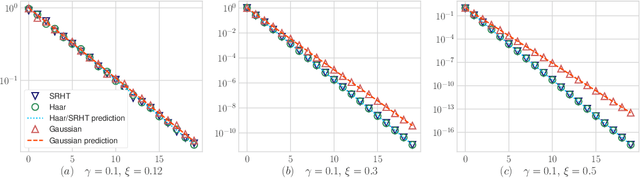
We provide an exact analysis of the limiting spectrum of matrices randomly projected either with the subsampled randomized Hadamard transform, or truncated Haar matrices. We characterize this limiting distribution through its Stieltjes transform, a classical object in random matrix theory, and compute the first and second inverse moments. We leverage the limiting spectrum and asymptotic freeness of random matrices to obtain an exact analysis of iterative sketching methods for solving least squares problems. Our results also yield optimal step-sizes and convergence rates in terms of simple closed-form expressions. Moreover, we show that the convergence rate for Haar and randomized Hadamard matrices are identical, and uniformly improve upon Gaussian random projections. The developed techniques and formulas can be applied to a plethora of randomized algorithms that employ fast randomized Hadamard dimension reduction.