Lethal Dose Conjecture on Data Poisoning
Paper and Code
Aug 05, 2022
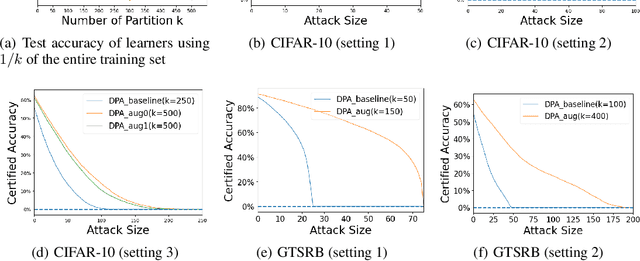
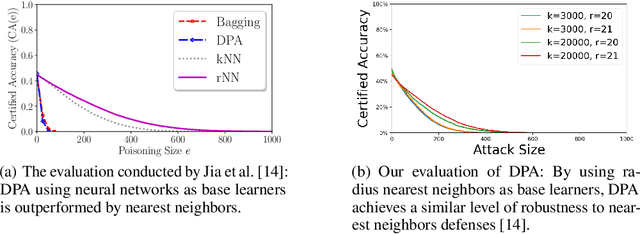
Data poisoning considers an adversary that distorts the training set of machine learning algorithms for malicious purposes. In this work, we bring to light one conjecture regarding the fundamentals of data poisoning, which we call the Lethal Dose Conjecture. The conjecture states: If $n$ clean training samples are needed for accurate predictions, then in a size-$N$ training set, only $\Theta(N/n)$ poisoned samples can be tolerated while ensuring accuracy. Theoretically, we verify this conjecture in multiple cases. We also offer a more general perspective of this conjecture through distribution discrimination. Deep Partition Aggregation (DPA) and its extension, Finite Aggregation (FA) are recent approaches for provable defenses against data poisoning, where they predict through the majority vote of many base models trained from different subsets of training set using a given learner. The conjecture implies that both DPA and FA are (asymptotically) optimal -- if we have the most data-efficient learner, they can turn it into one of the most robust defenses against data poisoning. This outlines a practical approach to developing stronger defenses against poisoning via finding data-efficient learners. Empirically, as a proof of concept, we show that by simply using different data augmentations for base learners, we can respectively double and triple the certified robustness of DPA on CIFAR-10 and GTSRB without sacrificing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge