Least Squares Approximation for a Distributed System

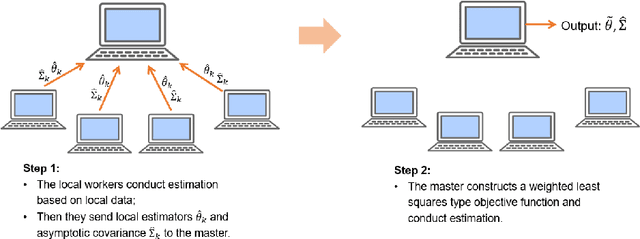
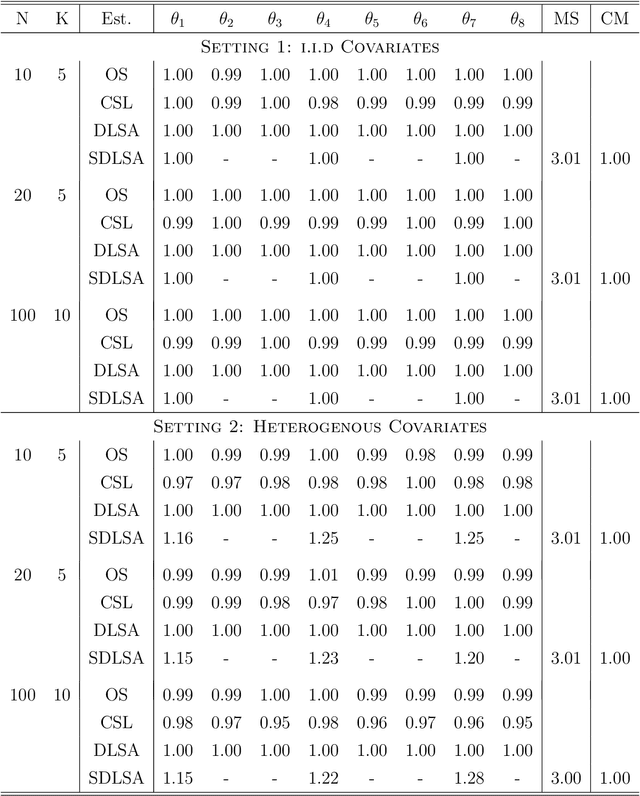
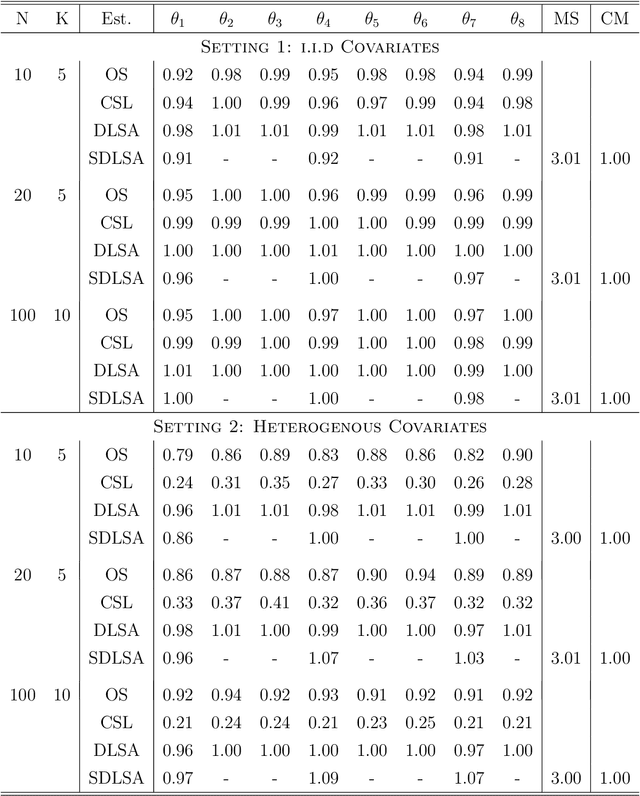
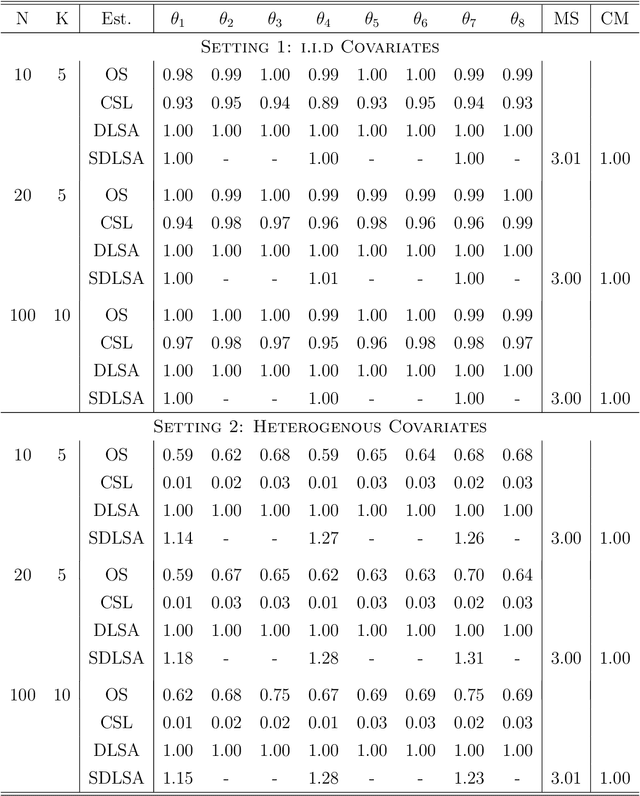
In this work we develop a distributed least squares approximation (DLSA) method, which is able to solve a large family of regression problems (e.g., linear regression, logistic regression, Cox's model) on a distributed system. By approximating the local objective function using a local quadratic form, we are able to obtain a combined estimator by taking a weighted average of local estimators. The resulting estimator is proved to be statistically as efficient as the global estimator. In the meanwhile it requires only one round of communication. We further conduct the shrinkage estimation based on the DLSA estimation by using an adaptive Lasso approach. The solution can be easily obtained by using the LARS algorithm on the master node. It is theoretically shown that the resulting estimator enjoys the oracle property and is selection consistent by using a newly designed distributed Bayesian Information Criterion (DBIC). The finite sample performance as well as the computational efficiency are further illustrated by extensive numerical study and an airline dataset. The airline dataset is 52GB in memory size. The entire methodology has been implemented by Python for a de-facto standard Spark system. By using the proposed DLSA algorithm on the Spark system, it takes 26 minutes to obtain a logistic regression estimator whereas a full likelihood algorithm takes 15 hours to reaches an inferior result.