Learning Universe Model for Partial Matching Networks over Multiple Graphs
Paper and Code
Oct 19, 2022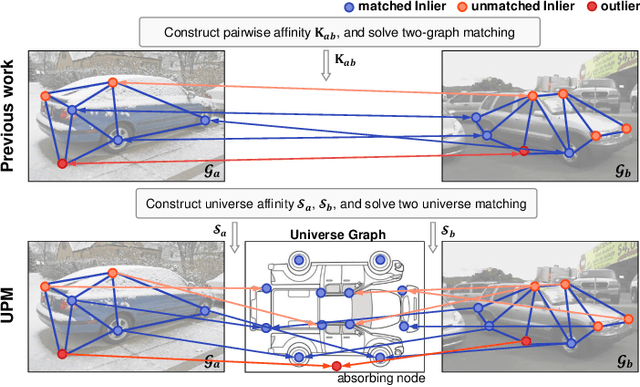



We consider the general setting for partial matching of two or multiple graphs, in the sense that not necessarily all the nodes in one graph can find their correspondences in another graph and vice versa. We take a universe matching perspective to this ubiquitous problem, whereby each node is either matched into an anchor in a virtual universe graph or regarded as an outlier. Such a universe matching scheme enjoys a few important merits, which have not been adopted in existing learning-based graph matching (GM) literature. First, the subtle logic for inlier matching and outlier detection can be clearly modeled, which is otherwise less convenient to handle in the pairwise matching scheme. Second, it enables end-to-end learning especially for universe level affinity metric learning for inliers matching, and loss design for gathering outliers together. Third, the resulting matching model can easily handle new arriving graphs under online matching, or even the graphs coming from different categories of the training set. To our best knowledge, this is the first deep learning network that can cope with two-graph matching, multiple-graph matching, online matching, and mixture graph matching simultaneously. Extensive experimental results show the state-of-the-art performance of our method in these settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge