Learning Unbiased Representations via Mutual Information Backpropagation
Paper and Code
Mar 13, 2020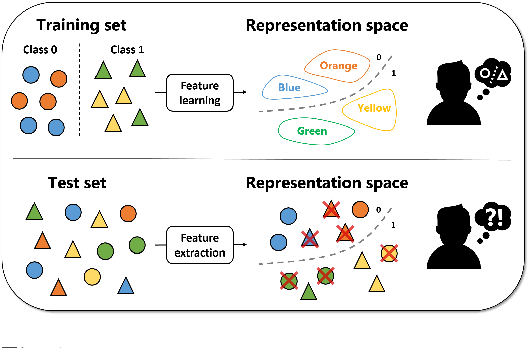
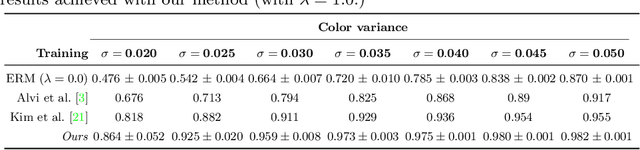
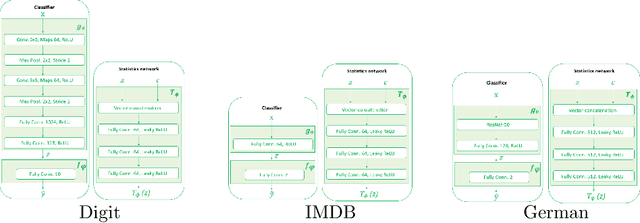
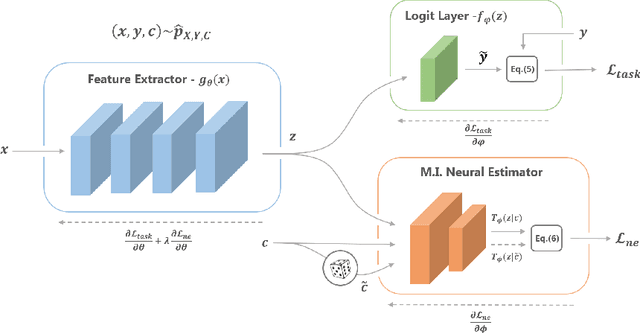
We are interested in learning data-driven representations that can generalize well, even when trained on inherently biased data. In particular, we face the case where some attributes (bias) of the data, if learned by the model, can severely compromise its generalization properties. We tackle this problem through the lens of information theory, leveraging recent findings for a differentiable estimation of mutual information. We propose a novel end-to-end optimization strategy, which simultaneously estimates and minimizes the mutual information between the learned representation and the data attributes. When applied on standard benchmarks, our model shows comparable or superior classification performance with respect to state-of-the-art approaches. Moreover, our method is general enough to be applicable to the problem of ``algorithmic fairness'', with competitive results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge