Learning Trembling Hand Perfect Mean Field Equilibrium for Dynamic Mean Field Games

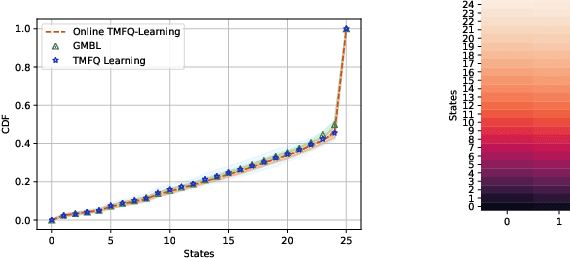
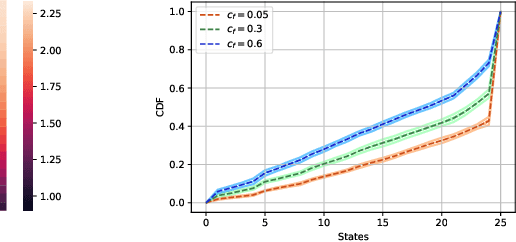
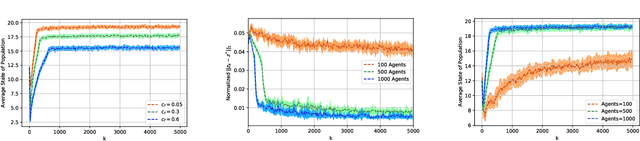
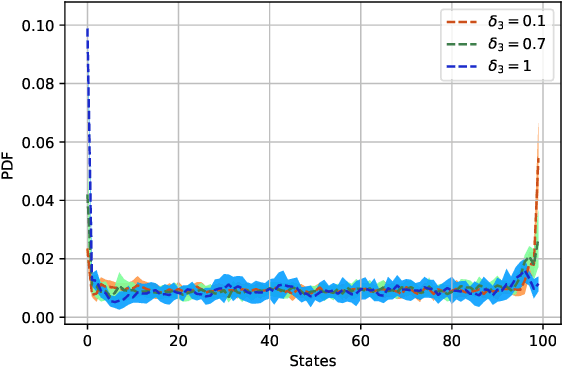
Mean Field Games (MFG) are those in which each agent assumes that the states of all others are drawn in an i.i.d. manner from a common belief distribution, and optimizes accordingly. The equilibrium concept here is a Mean Field Equilibrium (MFE), and algorithms for learning MFE in dynamic MFGs are unknown in general due to the non-stationary evolution of the belief distribution. Our focus is on an important subclass that possess a monotonicity property called Strategic Complementarities (MFG-SC). We introduce a natural refinement to the equilibrium concept that we call Trembling-Hand-Perfect MFE (T-MFE), which allows agents to employ a measure of randomization while accounting for the impact of such randomization on their payoffs. We propose a simple algorithm for computing T-MFE under a known model. We introduce both a model-free and a model based approach to learning T-MFE under unknown transition probabilities, using the trembling-hand idea of enabling exploration. We analyze the sample complexity of both algorithms. We also develop a scheme on concurrently sampling the system with a large number of agents that negates the need for a simulator, even though the model is non-stationary. Finally, we empirically evaluate the performance of the proposed algorithms via examples motivated by real-world applications.