Learning to swim in potential flow
Paper and Code
Sep 30, 2020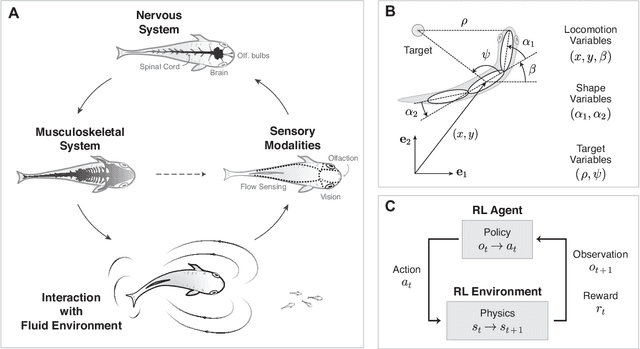
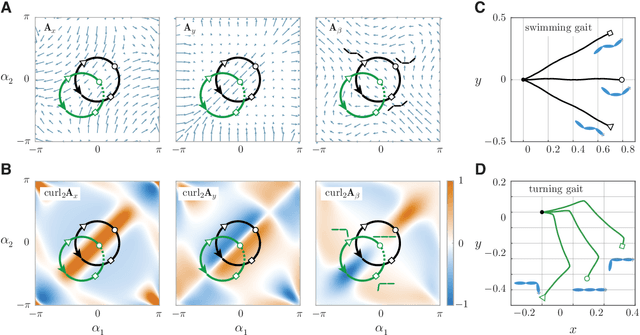
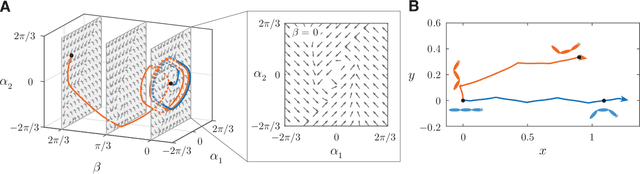
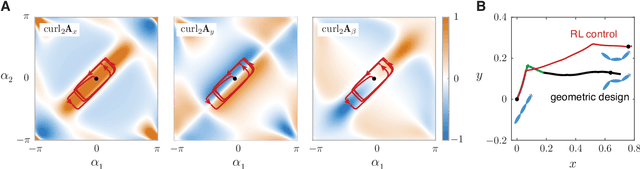
Fish swim by undulating their bodies. These propulsive motions require coordinated shape changes of a body that interacts with its fluid environment, but the specific shape coordination that leads to robust turning and swimming motions remains unclear. We propose a simple model of a three-link fish swimming in a potential flow environment and we use model-free reinforcement learning to arrive at optimal shape changes for two swimming tasks: swimming in a desired direction and swimming towards a known target. This fish model belongs to a class of problems in geometric mechanics, known as driftless dynamical systems, which allow us to analyze the swimming behavior in terms of geometric phases over the shape space of the fish. These geometric methods are less intuitive in the presence of drift. Here, we use the shape space analysis as a tool for assessing, visualizing, and interpreting the control policies obtained via reinforcement learning in the absence of drift. We then examine the robustness of these policies to drift-related perturbations. Although the fish has no direct control over the drift itself, it learns to take advantage of the presence of moderate drift to reach its target.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge