Learning to Generate 3D Shapes with Generative Cellular Automata
Paper and Code
Mar 06, 2021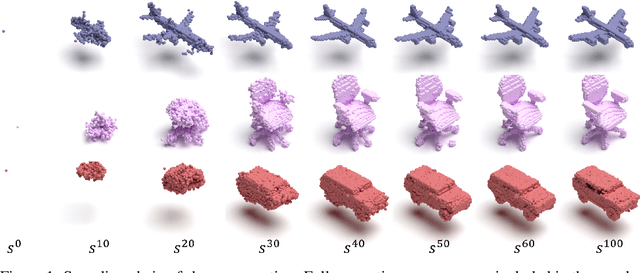
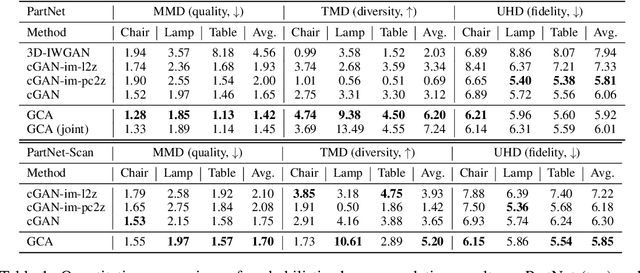
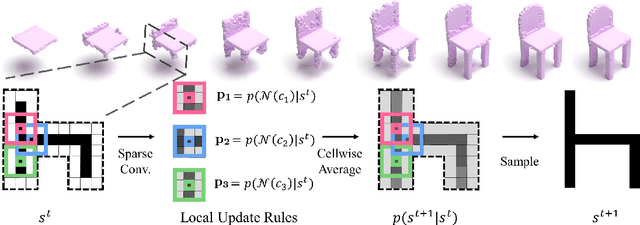
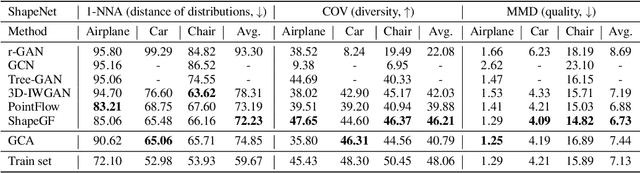
We present a probabilistic 3D generative model, named Generative Cellular Automata, which is able to produce diverse and high quality shapes. We formulate the shape generation process as sampling from the transition kernel of a Markov chain, where the sampling chain eventually evolves to the full shape of the learned distribution. The transition kernel employs the local update rules of cellular automata, effectively reducing the search space in a high-resolution 3D grid space by exploiting the connectivity and sparsity of 3D shapes. Our progressive generation only focuses on the sparse set of occupied voxels and their neighborhood, thus enabling the utilization of an expressive sparse convolutional network. We propose an effective training scheme to obtain the local homogeneous rule of generative cellular automata with sequences that are slightly different from the sampling chain but converge to the full shapes in the training data. Extensive experiments on probabilistic shape completion and shape generation demonstrate that our method achieves competitive performance against recent methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge