Learning to Combat Compounding-Error in Model-Based Reinforcement Learning
Paper and Code
Dec 24, 2019
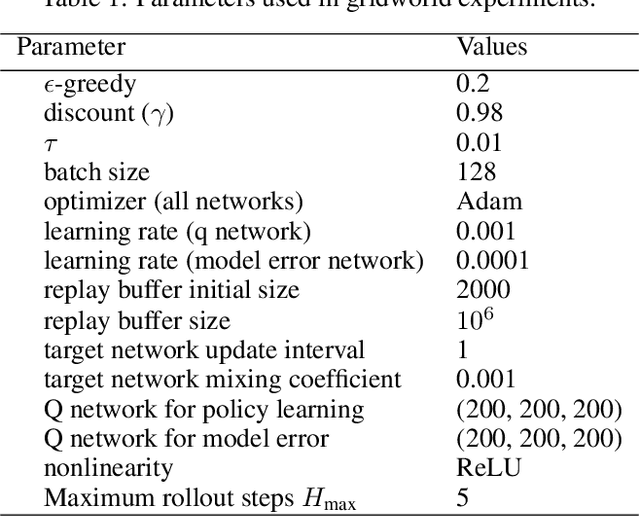
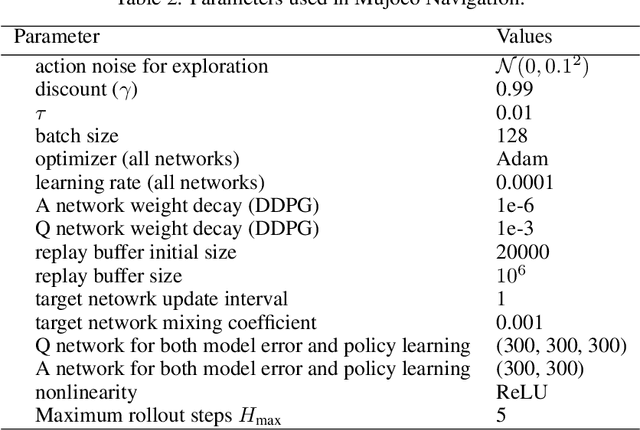
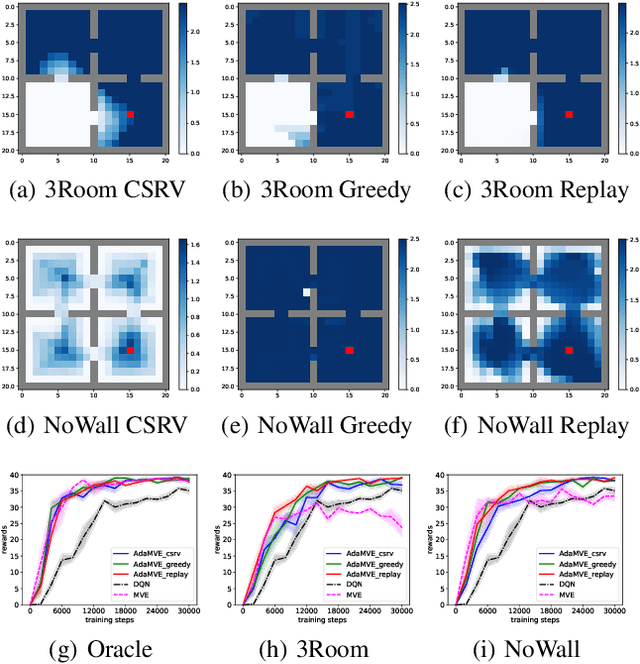
Despite its potential to improve sample complexity versus model-free approaches, model-based reinforcement learning can fail catastrophically if the model is inaccurate. An algorithm should ideally be able to trust an imperfect model over a reasonably long planning horizon, and only rely on model-free updates when the model errors get infeasibly large. In this paper, we investigate techniques for choosing the planning horizon on a state-dependent basis, where a state's planning horizon is determined by the maximum cumulative model error around that state. We demonstrate that these state-dependent model errors can be learned with Temporal Difference methods, based on a novel approach of temporally decomposing the cumulative model errors. Experimental results show that the proposed method can successfully adapt the planning horizon to account for state-dependent model accuracy, significantly improving the efficiency of policy learning compared to model-based and model-free baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge