Learning the Uncertainty Sets for Control Dynamics via Set Membership: A Non-Asymptotic Analysis

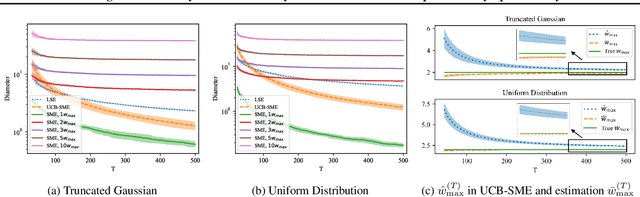
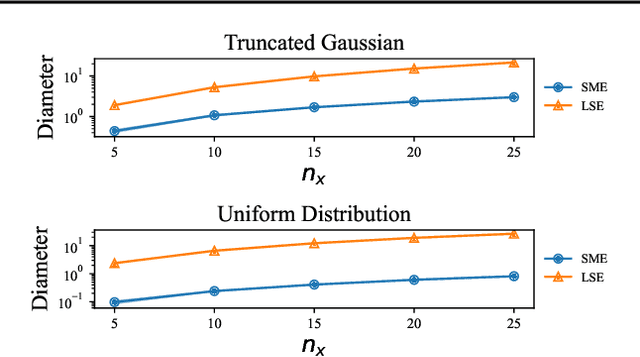
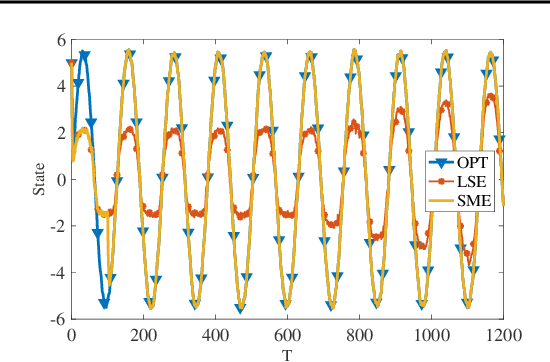
Set-membership estimation is commonly used in adaptive/learning-based control algorithms that require robustness over the model uncertainty sets, e.g., online robustly stabilizing control and robust adaptive model predictive control. Despite having broad applications, non-asymptotic estimation error bounds in the stochastic setting are limited. This paper provides such a non-asymptotic bound on the diameter of the uncertainty sets generated by set membership estimation on linear dynamical systems under bounded, i.i.d. disturbances. Further, this result is applied to robust adaptive model predictive control with uncertainty sets updated by set membership. We numerically demonstrate the performance of the robust adaptive controller, which rapidly approaches the performance of the offline optimal model predictive controller, in comparison with the control design based on least square estimation's confidence regions.