Learning Solution Manifolds for Control Problems via Energy Minimization
Paper and Code
Mar 07, 2022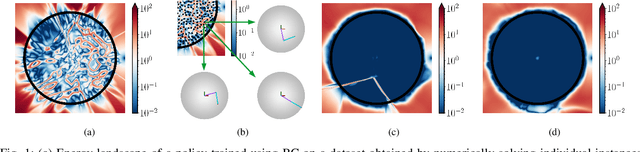
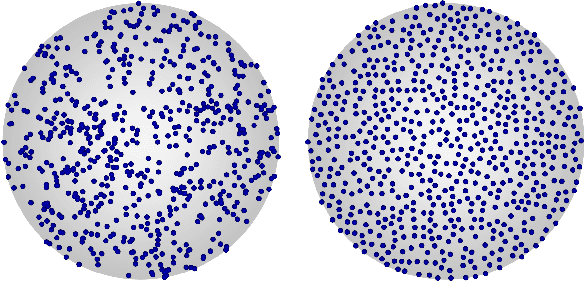
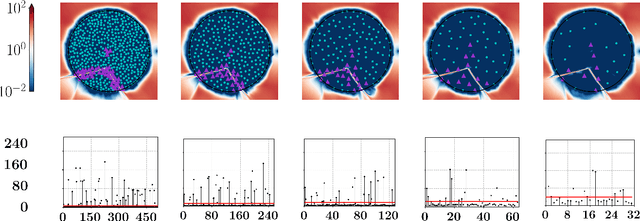
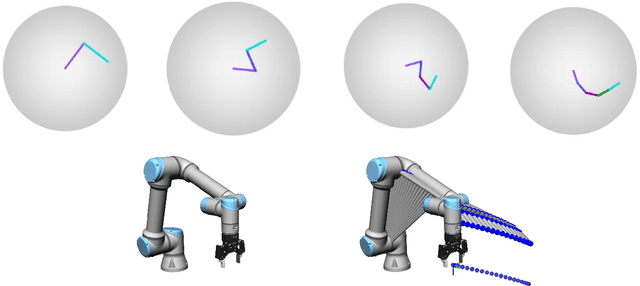
A variety of control tasks such as inverse kinematics (IK), trajectory optimization (TO), and model predictive control (MPC) are commonly formulated as energy minimization problems. Numerical solutions to such problems are well-established. However, these are often too slow to be used directly in real-time applications. The alternative is to learn solution manifolds for control problems in an offline stage. Although this distillation process can be trivially formulated as a behavioral cloning (BC) problem in an imitation learning setting, our experiments highlight a number of significant shortcomings arising due to incompatible local minima, interpolation artifacts, and insufficient coverage of the state space. In this paper, we propose an alternative to BC that is efficient and numerically robust. We formulate the learning of solution manifolds as a minimization of the energy terms of a control objective integrated over the space of problems of interest. We minimize this energy integral with a novel method that combines Monte Carlo-inspired adaptive sampling strategies with the derivatives used to solve individual instances of the control task. We evaluate the performance of our formulation on a series of robotic control problems of increasing complexity, and we highlight its benefits through comparisons against traditional methods such as behavioral cloning and Dataset aggregation (Dagger).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge