Learning Simple Thresholded Features with Sparse Support Recovery

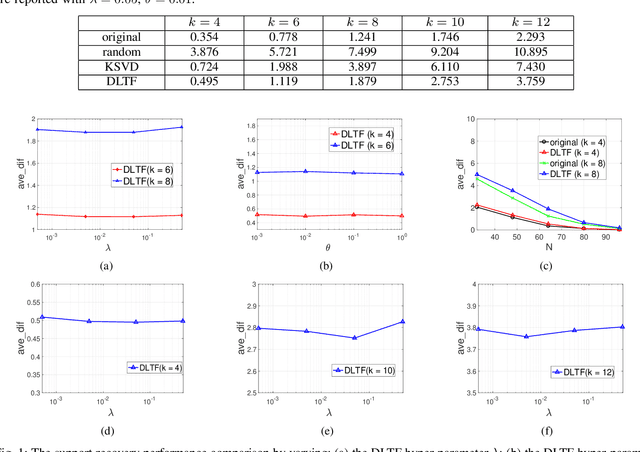
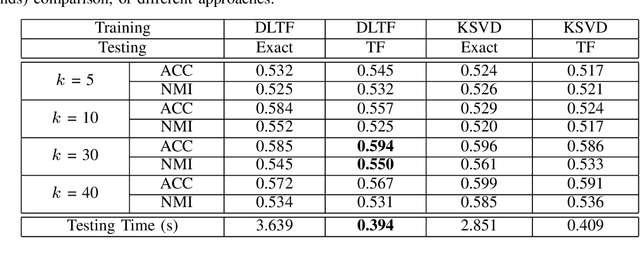
The thresholded feature has recently emerged as an extremely efficient, yet rough empirical approximation, of the time-consuming sparse coding inference process. Such an approximation has not yet been rigorously examined, and standard dictionaries often lead to non-optimal performance when used for computing thresholded features. In this paper, we first present two theoretical recovery guarantees for the thresholded feature to exactly recover the nonzero support of the sparse code. Motivated by them, we then formulate the Dictionary Learning for Thresholded Features (DLTF) model, which learns an optimized dictionary for applying the thresholded feature. In particular, for the $(k, 2)$ norm involved, a novel proximal operator with log-linear time complexity $O(m\log m)$ is derived. We evaluate the performance of DLTF on a vast range of synthetic and real-data tasks, where DLTF demonstrates remarkable efficiency, effectiveness and robustness in all experiments. In addition, we briefly discuss the potential link between DLTF and deep learning building blocks.