Learning quantum dynamics with latent neural ODEs

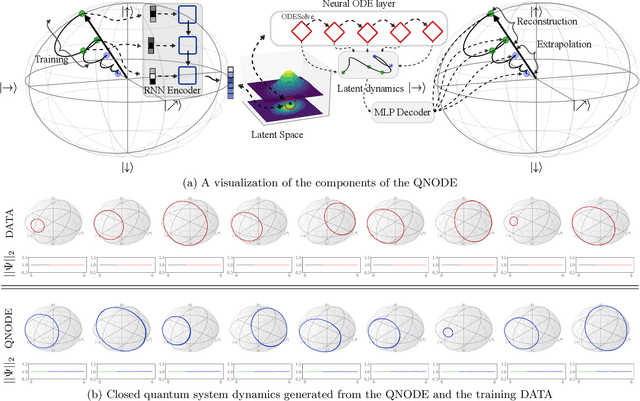
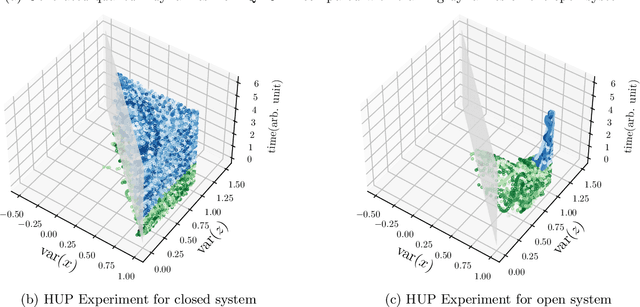
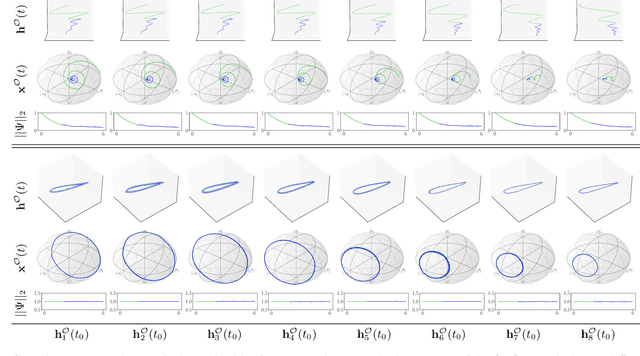
The core objective of machine-assisted scientific discovery is to learn physical laws from experimental data without prior knowledge of the systems in question. In the area of quantum physics, making progress towards these goals is significantly more challenging due to the curse of dimensionality as well as the counter-intuitive nature of quantum mechanics. Here, we present the QNODE, a latent neural ODE trained on dynamics from closed and open quantum systems. The QNODE can learn to generate quantum dynamics and extrapolate outside of its training region that satisfy the von Neumann and time-local Lindblad master equations for closed and open quantum systems. Furthermore the QNODE rediscovers quantum mechanical laws such as Heisenberg's uncertainty principle in a totally data-driven way, without constraints or guidance. Additionally, we show that trajectories that are generated from the QNODE and are close in its latent space have similar quantum dynamics while preserving the physics of the training system.