Learning Partial Differential Equations with Deep Parallel Neural Operators
Paper and Code
Sep 30, 2024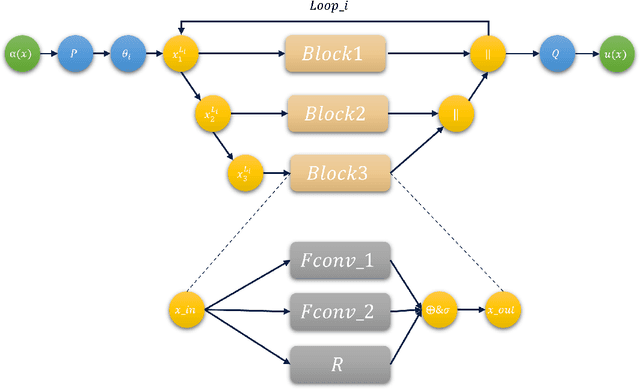



In recent years, Solving partial differential equations has shifted the focus of traditional neural network studies from finite-dimensional Euclidean spaces to generalized functional spaces in research. A novel methodology is to learn an operator as a means of approximating the mapping between outputs. Currently, researchers have proposed a variety of operator architectures. Nevertheless, the majority of these architectures adopt an iterative update architecture, whereby a single operator is learned from the same function space. In practical physical science problems, the numerical solutions of partial differential equations are complex, and a serial single operator is unable to accurately approximate the intricate mapping between input and output. So, We propose a deep parallel operator model (DPNO) for efficiently and accurately solving partial differential equations. DPNO employs convolutional neural networks to extract local features and map data into distinct latent spaces. Designing a parallel block of double Fourier neural operators to solve the iterative error problem. DPNO approximates complex mappings between inputs and outputs by learning multiple operators in different potential spaces in parallel blocks. DPNO achieved the best performance on five of them, with an average improvement of 10.5\%, and ranked second on one dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge