Learning Neural Networks with Adaptive Regularization
Paper and Code
Jul 14, 2019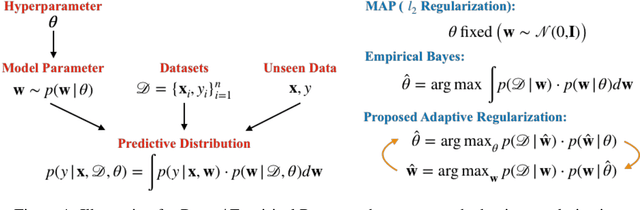
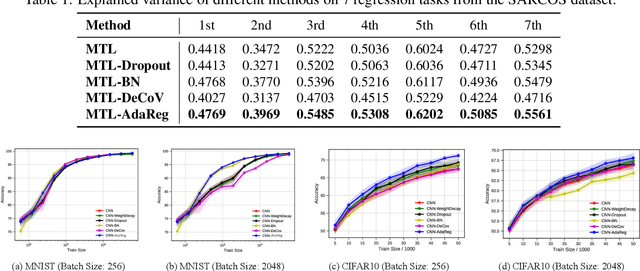
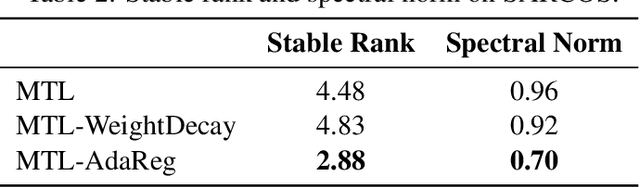
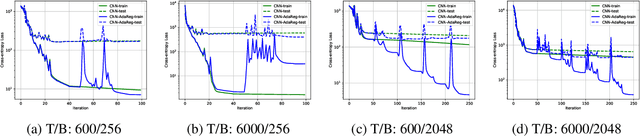
Feed-forward neural networks can be understood as a combination of an intermediate representation and a linear hypothesis. While most previous works aim to diversify the representations, we explore the complementary direction by performing an adaptive and data-dependent regularization motivated by the empirical Bayes method. Specifically, we propose to construct a matrix-variate normal prior (on weights) whose covariance matrix has a Kronecker product structure. This structure is designed to capture the correlations in neurons through backpropagation. Under the assumption of this Kronecker factorization, the prior encourages neurons to borrow statistical strength from one another. Hence, it leads to an adaptive and data-dependent regularization when training networks on small datasets. To optimize the model, we present an efficient block coordinate descent algorithm with analytical solutions. Empirically, we demonstrate that the proposed method helps networks converge to local optima with smaller stable ranks and spectral norms. These properties suggest better generalizations and we present empirical results to support this expectation. We also verify the effectiveness of the approach on multiclass classification and multitask regression problems with various network structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge