Learning Nash Equilibria in Zero-Sum Stochastic Games via Entropy-Regularized Policy Approximation

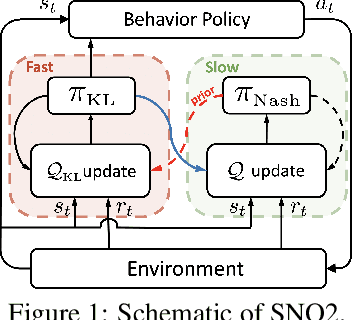
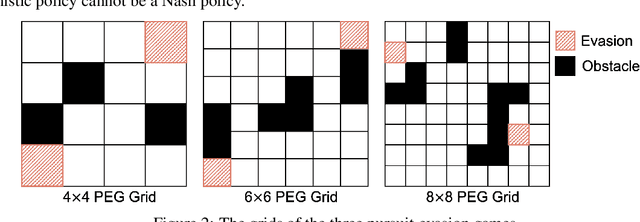
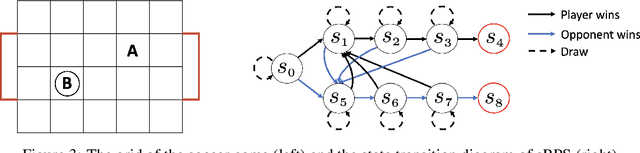
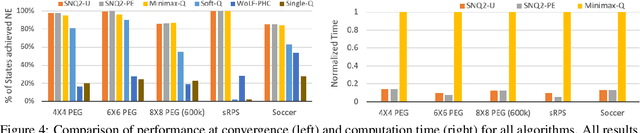
We explore the use of policy approximation for reducing the computational cost of learning Nash equilibria in multi-agent reinforcement learning scenarios. We propose a new algorithm for zero-sum stochastic games in which each agent simultaneously learns a Nash policy and an entropy-regularized policy. The two policies help each other towards convergence: the former guides the latter to the desired Nash equilibrium, while the latter serves as an efficient approximation of the former. We demonstrate the possibility of using the proposed algorithm to transfer previous training experiences to different environments, enabling the agents to adapt quickly to new tasks. We also provide a dynamic hyper-parameter scheduling scheme for further expedited convergence. Empirical results applied to a number of stochastic games show that the proposed algorithm converges to the Nash equilibrium while exhibiting a major speed-up over existing algorithms.