Learning Multiple Levels of Representations with Kernel Machines

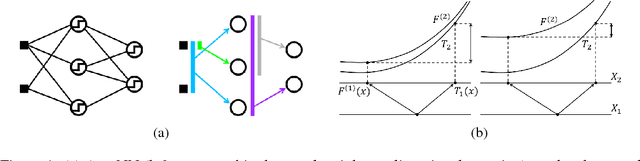
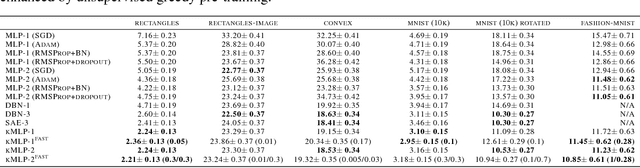
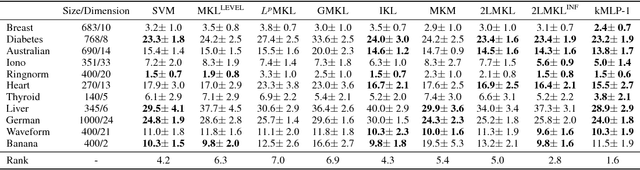
We propose a connectionist-inspired kernel machine model with three key advantages over traditional kernel machines. First, it is capable of learning distributed and hierarchical representations. Second, its performance is highly robust to the choice of kernel function. Third, the solution space is not limited to the span of images of training data in reproducing kernel Hilbert space (RKHS). Together with the architecture, we propose a greedy learning algorithm that allows the proposed multilayer network to be trained layer-wise without backpropagation by optimizing the geometric properties of images in RKHS. With a single fixed generic kernel for each layer and two layers in total, our model compares favorably with state-of-the-art multiple kernel learning algorithms using significantly more kernels and popular deep architectures on widely used classification benchmarks.