Learning Generative Models with Sinkhorn Divergences
Paper and Code
Oct 20, 2017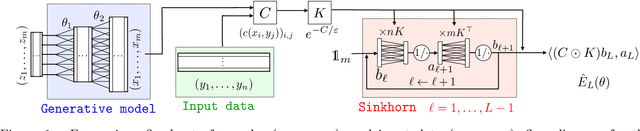
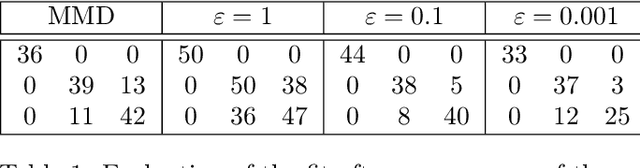
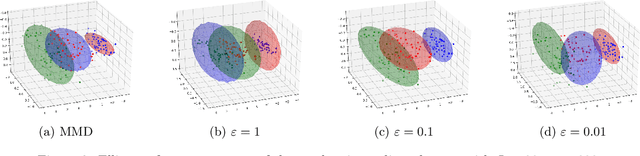

The ability to compare two degenerate probability distributions (i.e. two probability distributions supported on two distinct low-dimensional manifolds living in a much higher-dimensional space) is a crucial problem arising in the estimation of generative models for high-dimensional observations such as those arising in computer vision or natural language. It is known that optimal transport metrics can represent a cure for this problem, since they were specifically designed as an alternative to information divergences to handle such problematic scenarios. Unfortunately, training generative machines using OT raises formidable computational and statistical challenges, because of (i) the computational burden of evaluating OT losses, (ii) the instability and lack of smoothness of these losses, (iii) the difficulty to estimate robustly these losses and their gradients in high dimension. This paper presents the first tractable computational method to train large scale generative models using an optimal transport loss, and tackles these three issues by relying on two key ideas: (a) entropic smoothing, which turns the original OT loss into one that can be computed using Sinkhorn fixed point iterations; (b) algorithmic (automatic) differentiation of these iterations. These two approximations result in a robust and differentiable approximation of the OT loss with streamlined GPU execution. Entropic smoothing generates a family of losses interpolating between Wasserstein (OT) and Maximum Mean Discrepancy (MMD), thus allowing to find a sweet spot leveraging the geometry of OT and the favorable high-dimensional sample complexity of MMD which comes with unbiased gradient estimates. The resulting computational architecture complements nicely standard deep network generative models by a stack of extra layers implementing the loss function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge