Learning from History for Byzantine Robust Optimization

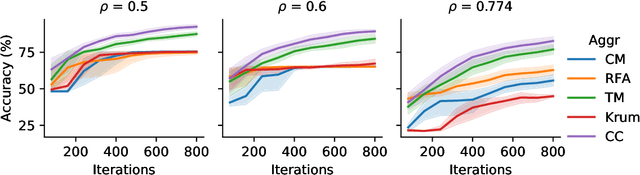
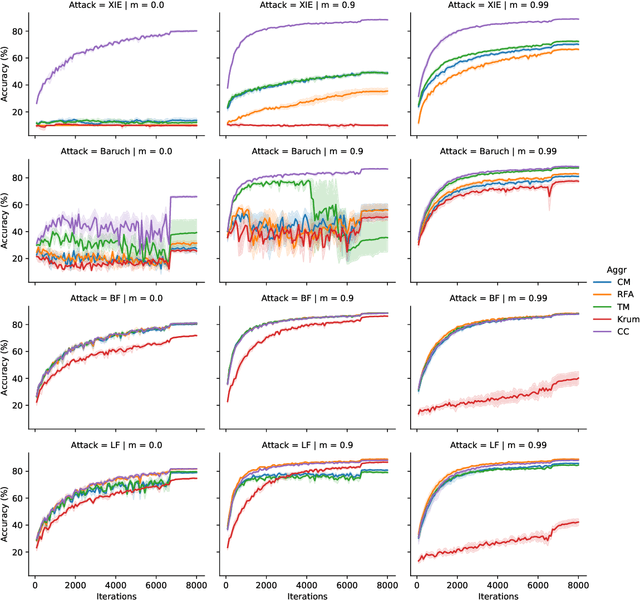
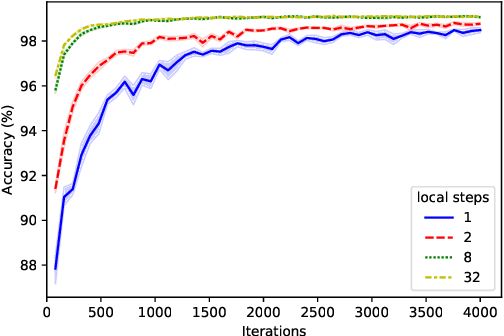
Byzantine robustness has received significant attention recently given its importance for distributed and federated learning. In spite of this, we identify severe flaws in existing algorithms even when the data across the participants is assumed to be identical. First, we show that most existing robust aggregation rules may not converge even in the absence of any Byzantine attackers, because they are overly sensitive to the distribution of the noise in the stochastic gradients. Secondly, we show that even if the aggregation rules may succeed in limiting the influence of the attackers in a single round, the attackers can couple their attacks across time eventually leading to divergence. To address these issues, we present two surprisingly simple strategies: a new iterative clipping procedure, and incorporating worker momentum to overcome time-coupled attacks. This is the first provably robust method for the standard stochastic non-convex optimization setting.