Learning Finite Linear Temporal Logic Specifications with a Specialized Neural Operator
Paper and Code
Nov 21, 2021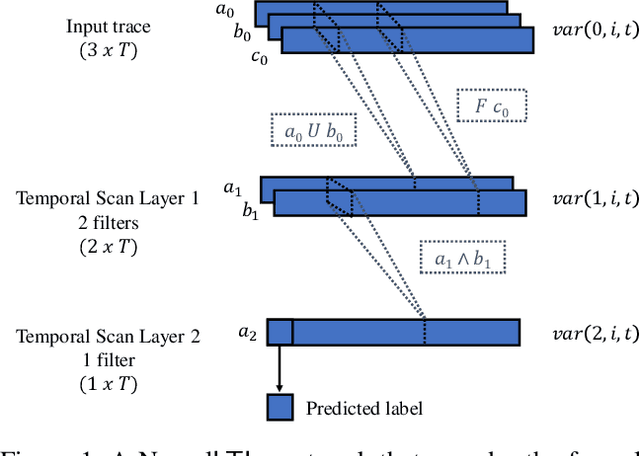
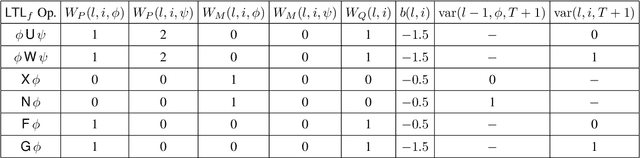

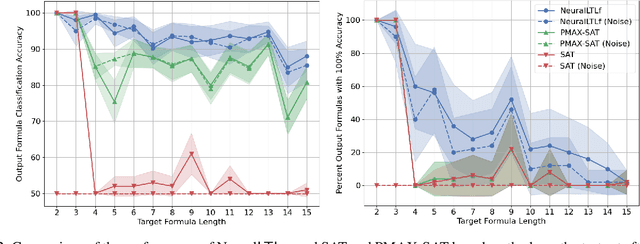
Finite linear temporal logic ($\mathsf{LTL}_f$) is a powerful formal representation for modeling temporal sequences. We address the problem of learning a compact $\mathsf{LTL}_f$ formula from labeled traces of system behavior. We propose a novel neural network operator and evaluate the resulting architecture, Neural$\mathsf{LTL}_f$. Our approach includes a specialized recurrent filter, designed to subsume $\mathsf{LTL}_f$ temporal operators, to learn a highly accurate classifier for traces. Then, it discretizes the activations and extracts the truth table represented by the learned weights. This truth table is converted to symbolic form and returned as the learned formula. Experiments on randomly generated $\mathsf{LTL}_f$ formulas show Neural$\mathsf{LTL}_f$ scales to larger formula sizes than existing approaches and maintains high accuracy even in the presence of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge