Learning Efficient Constraint Graph Sampling for Robotic Sequential Manipulation
Paper and Code
Nov 09, 2020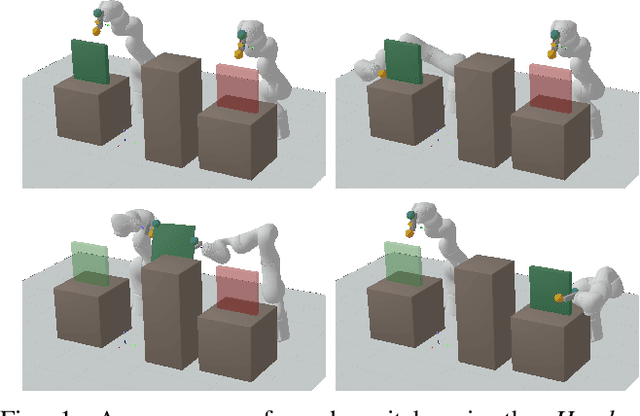
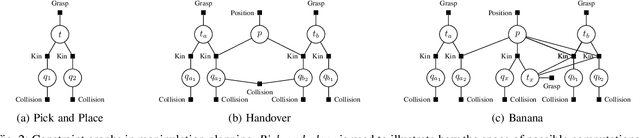
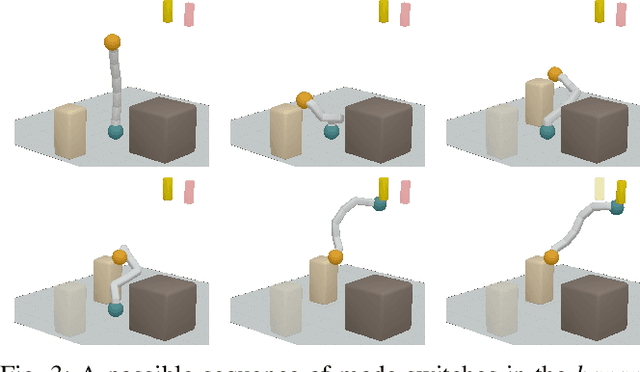
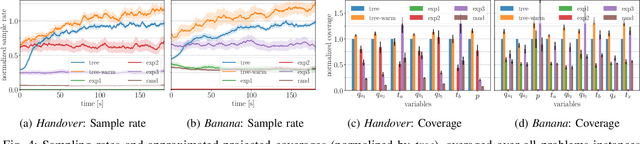
Efficient sampling from constraint manifolds, and thereby generating a diverse set of solutions of feasibility problems, is a fundamental challenge. We consider the case where a problem is factored, that is, the underlying nonlinear mathematical program is decomposed into differentiable equality and inequality constraints, each of which depends only on some variables. Such problems are at the core of efficient and robust sequential robot manipulation planning. Naive sequential conditional sampling of individual variables, as well as fully joint sampling of all variables at once (e.g., leveraging optimization methods), can be highly inefficient and non-robust. We propose a novel framework to learn how to break the overall problem into smaller sequential sampling problems. Specifically, we leverage Monte-Carlo Tree Search to learn which variable subsets should be assigned in which sequential order, in order to minimize the computation time to generate full samples. This strategy allows us to efficiently compute a set of diverse valid robot configurations for mode-switches within sequential manipulation tasks, which are waypoints for subsequent trajectory optimization or sampling-based motion planning algorithms. We show that the learning method quickly converges to the best sampling strategy for a given problem, and outperforms user-defined orderings and joint optimization, while also providing a higher sample diversity. Video: https://youtu.be/xWAjBGACZhs
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge