Learning ECG signal features without backpropagation
Paper and Code
Jul 04, 2023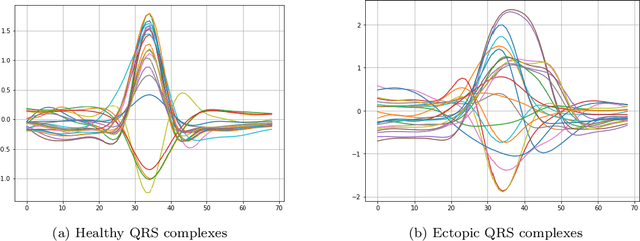
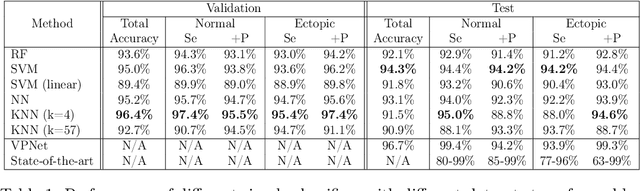
Representation learning has become a crucial area of research in machine learning, as it aims to discover efficient ways of representing raw data with useful features to increase the effectiveness, scope and applicability of downstream tasks such as classification and prediction. In this paper, we propose a novel method to generate representations for time series-type data. This method relies on ideas from theoretical physics to construct a compact representation in a data-driven way, and it can capture both the underlying structure of the data and task-specific information while still remaining intuitive, interpretable and verifiable. This novel methodology aims to identify linear laws that can effectively capture a shared characteristic among samples belonging to a specific class. By subsequently utilizing these laws to generate a classifier-agnostic representation in a forward manner, they become applicable in a generalized setting. We demonstrate the effectiveness of our approach on the task of ECG signal classification, achieving state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge