Learning Differentiable Safety-Critical Control using Control Barrier Functions for Generalization to Novel Environments

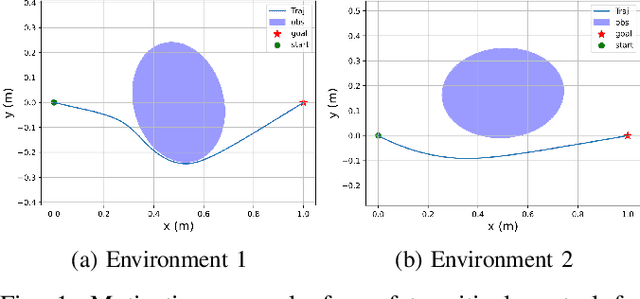
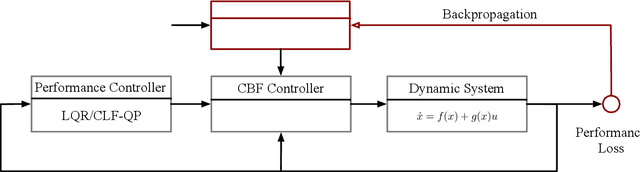
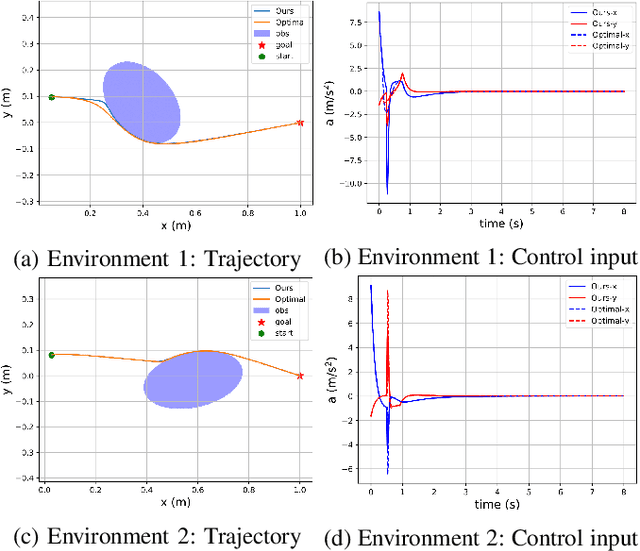
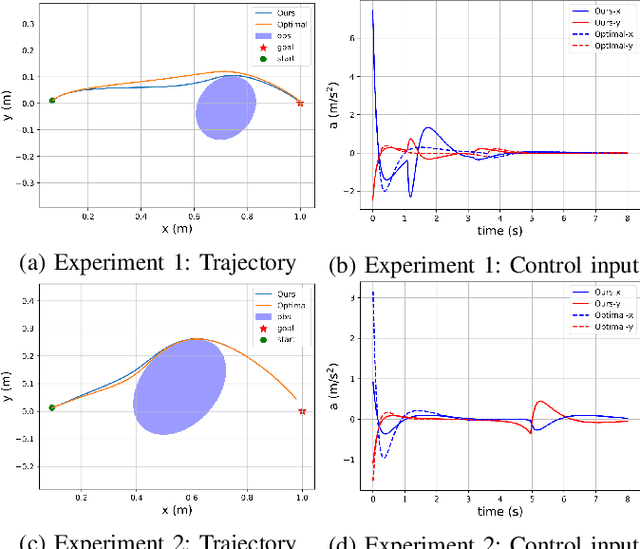
Control barrier functions (CBFs) have become a popular tool to enforce safety of a control system. CBFs are commonly utilized in a quadratic program formulation (CBF-QP) as safety-critical constraints. A class $\mathcal{K}$ function in CBFs usually needs to be tuned manually in order to balance the trade-off between performance and safety for each environment. However, this process is often heuristic and can become intractable for high relative-degree systems. Moreover, it prevents the CBF-QP from generalizing to different environments in the real world. By embedding the optimization procedure of the CBF-QP as a differentiable layer within a deep learning architecture, we propose a differentiable optimization-based safety-critical control framework that enables generalization to new environments with forward invariance guarantees. Finally, we validate the proposed control design with 2D double and quadruple integrator systems in various environments.