Learning Baseline Values for Shapley Values
Paper and Code
May 22, 2021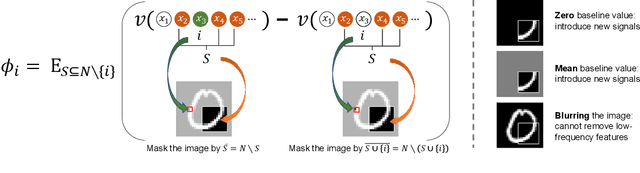



This paper aims to formulate the problem of estimating the optimal baseline values for the Shapley value in game theory. The Shapley value measures the attribution of each input variable of a complex model, which is computed as the marginal benefit from the presence of this variable w.r.t.its absence under different contexts. To this end, people usually set the input variable to its baseline value to represent the absence of this variable (i.e.the no-signal state of this variable). Previous studies usually determine the baseline values in an empirical manner, which hurts the trustworthiness of the Shapley value. In this paper, we revisit the feature representation of a deep model from the perspective of game theory, and define the multi-variate interaction patterns of input variables to define the no-signal state of an input variable. Based on the multi-variate interaction, we learn the optimal baseline value of each input variable. Experimental results have demonstrated the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge