Learning and Meshing from Deep Implicit Surface Networks Using an Efficient Implementation of Analytic Marching
Paper and Code
Jun 18, 2021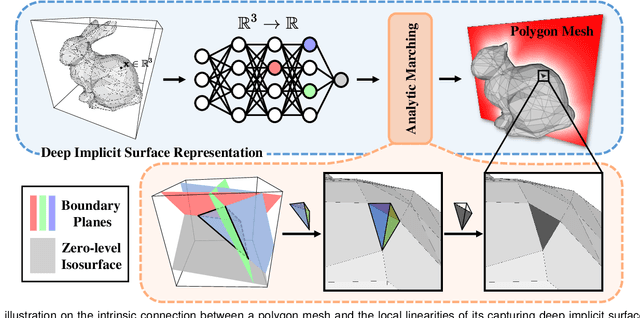
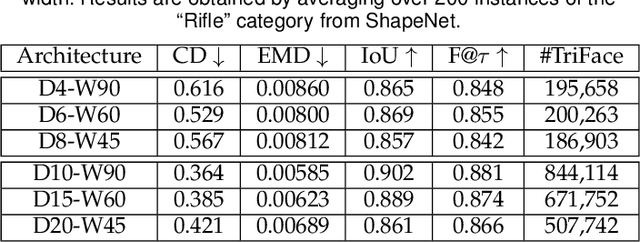
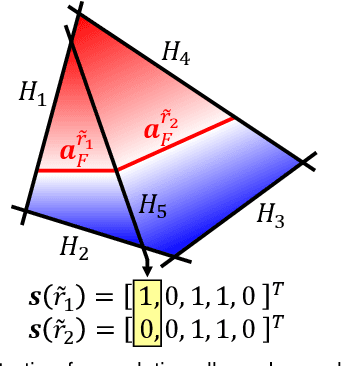
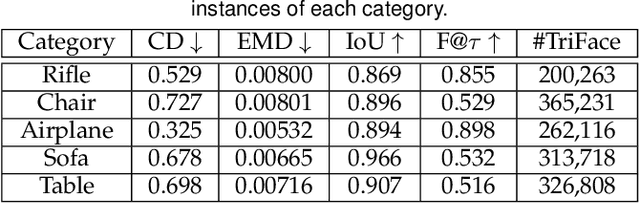
Reconstruction of object or scene surfaces has tremendous applications in computer vision, computer graphics, and robotics. In this paper, we study a fundamental problem in this context about recovering a surface mesh from an implicit field function whose zero-level set captures the underlying surface. To achieve the goal, existing methods rely on traditional meshing algorithms; while promising, they suffer from loss of precision learned in the implicit surface networks, due to the use of discrete space sampling in marching cubes. Given that an MLP with activations of Rectified Linear Unit (ReLU) partitions its input space into a number of linear regions, we are motivated to connect this local linearity with a same property owned by the desired result of polygon mesh. More specifically, we identify from the linear regions, partitioned by an MLP based implicit function, the analytic cells and analytic faces that are associated with the function's zero-level isosurface. We prove that under mild conditions, the identified analytic faces are guaranteed to connect and form a closed, piecewise planar surface. Based on the theorem, we propose an algorithm of analytic marching, which marches among analytic cells to exactly recover the mesh captured by an implicit surface network. We also show that our theory and algorithm are equally applicable to advanced MLPs with shortcut connections and max pooling. Given the parallel nature of analytic marching, we contribute AnalyticMesh, a software package that supports efficient meshing of implicit surface networks via CUDA parallel computing, and mesh simplification for efficient downstream processing. We apply our method to different settings of generative shape modeling using implicit surface networks. Extensive experiments demonstrate our advantages over existing methods in terms of both meshing accuracy and efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge