Learning Accurate and Interpretable Decision Rule Sets from Neural Networks
Paper and Code
Mar 12, 2021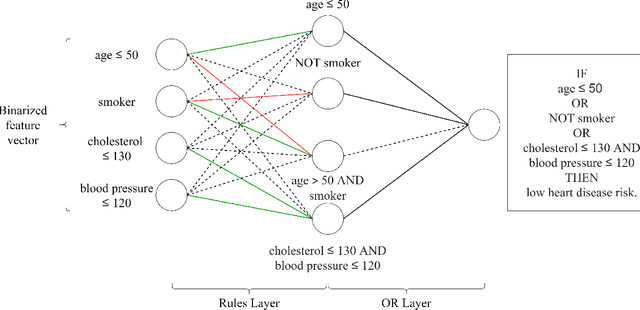
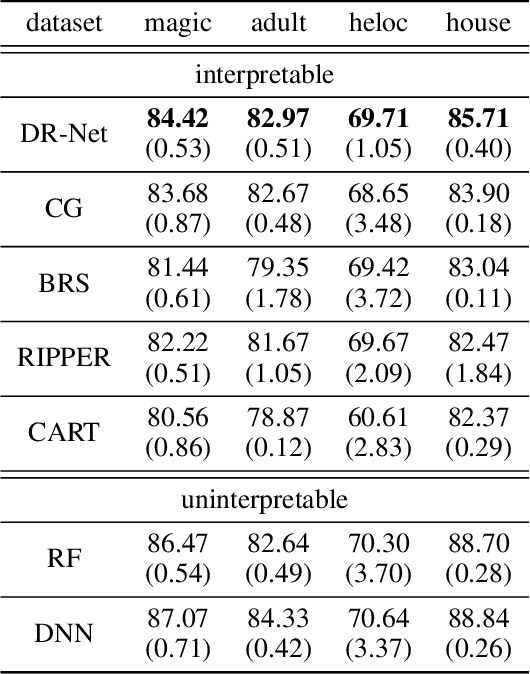
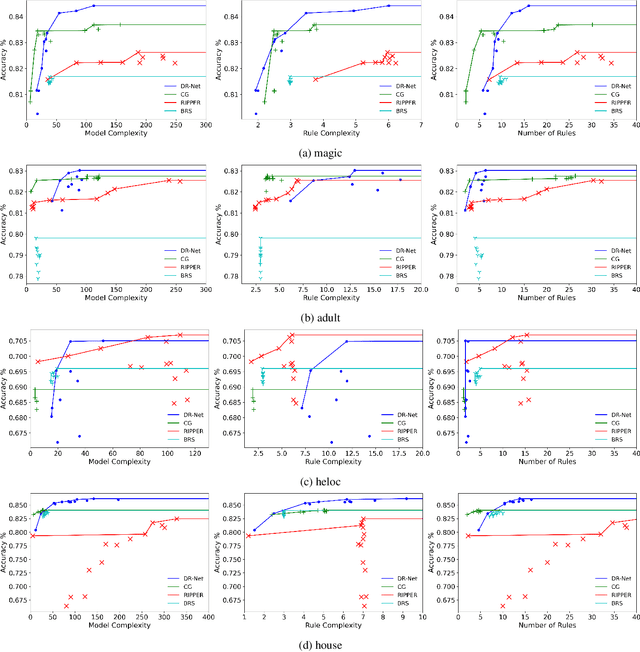

This paper proposes a new paradigm for learning a set of independent logical rules in disjunctive normal form as an interpretable model for classification. We consider the problem of learning an interpretable decision rule set as training a neural network in a specific, yet very simple two-layer architecture. Each neuron in the first layer directly maps to an interpretable if-then rule after training, and the output neuron in the second layer directly maps to a disjunction of the first-layer rules to form the decision rule set. Our representation of neurons in this first rules layer enables us to encode both the positive and the negative association of features in a decision rule. State-of-the-art neural net training approaches can be leveraged for learning highly accurate classification models. Moreover, we propose a sparsity-based regularization approach to balance between classification accuracy and the simplicity of the derived rules. Our experimental results show that our method can generate more accurate decision rule sets than other state-of-the-art rule-learning algorithms with better accuracy-simplicity trade-offs. Further, when compared with uninterpretable black-box machine learning approaches such as random forests and full-precision deep neural networks, our approach can easily find interpretable decision rule sets that have comparable predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge