Latent Schrodinger Bridge: Prompting Latent Diffusion for Fast Unpaired Image-to-Image Translation

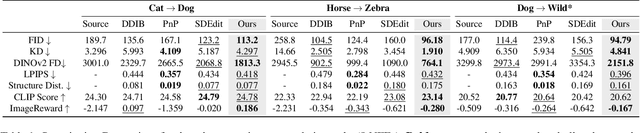
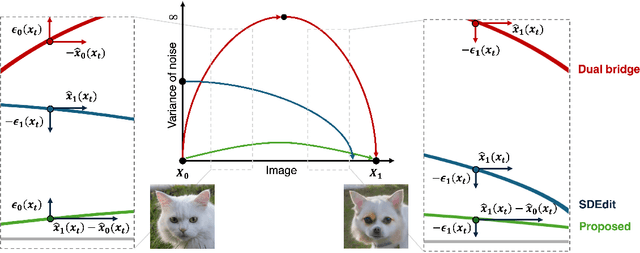
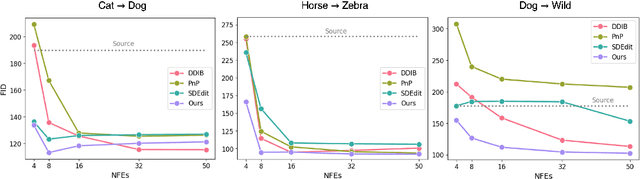
Diffusion models (DMs), which enable both image generation from noise and inversion from data, have inspired powerful unpaired image-to-image (I2I) translation algorithms. However, they often require a larger number of neural function evaluations (NFEs), limiting their practical applicability. In this paper, we tackle this problem with Schrodinger Bridges (SBs), which are stochastic differential equations (SDEs) between distributions with minimal transport cost. We analyze the probability flow ordinary differential equation (ODE) formulation of SBs, and observe that we can decompose its vector field into a linear combination of source predictor, target predictor, and noise predictor. Inspired by this observation, we propose Latent Schrodinger Bridges (LSBs) that approximate the SB ODE via pre-trained Stable Diffusion, and develop appropriate prompt optimization and change of variables formula to match the training and inference between distributions. We demonstrate that our algorithm successfully conduct competitive I2I translation in unsupervised setting with only a fraction of computation cost required by previous DM-based I2I methods.