Large-Margin Determinantal Point Processes
Paper and Code
Nov 07, 2014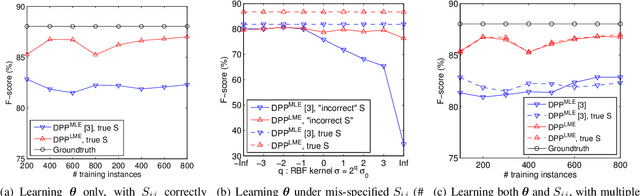


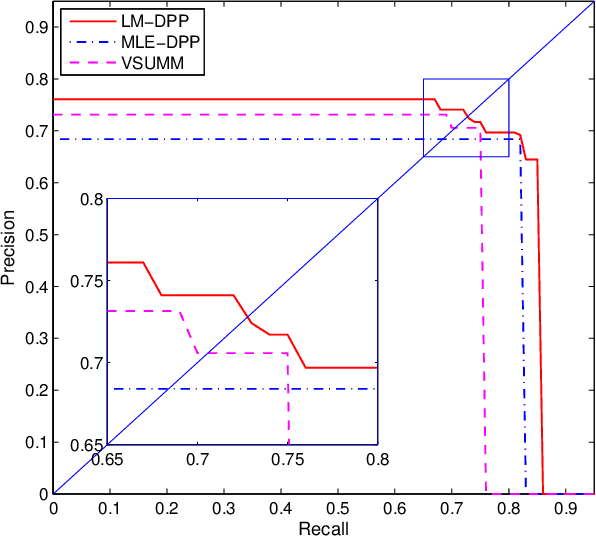
Determinantal point processes (DPPs) offer a powerful approach to modeling diversity in many applications where the goal is to select a diverse subset. We study the problem of learning the parameters (the kernel matrix) of a DPP from labeled training data. We make two contributions. First, we show how to reparameterize a DPP's kernel matrix with multiple kernel functions, thus enhancing modeling flexibility. Second, we propose a novel parameter estimation technique based on the principle of large margin separation. In contrast to the state-of-the-art method of maximum likelihood estimation, our large-margin loss function explicitly models errors in selecting the target subsets, and it can be customized to trade off different types of errors (precision vs. recall). Extensive empirical studies validate our contributions, including applications on challenging document and video summarization, where flexibility in modeling the kernel matrix and balancing different errors is indispensable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge