Laplacian-based Cluster-Contractive t-SNE for High Dimensional Data Visualization
Paper and Code
Jul 25, 2022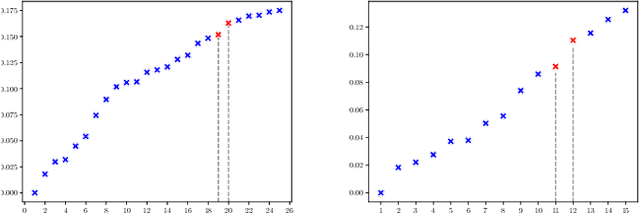

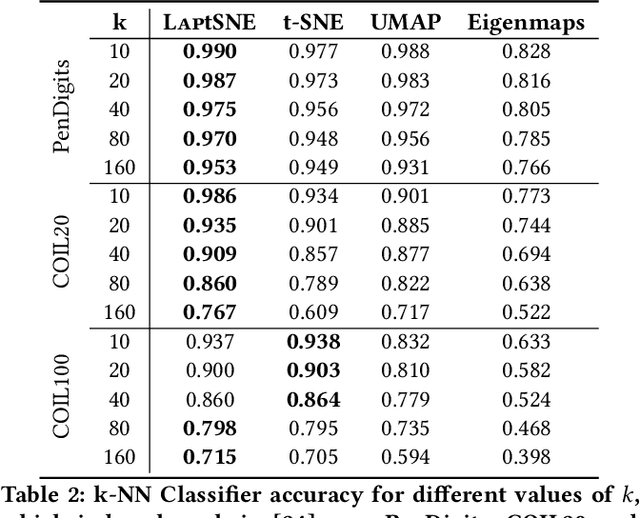

Dimensionality reduction techniques aim at representing high-dimensional data in low-dimensional spaces to extract hidden and useful information or facilitate visual understanding and interpretation of the data. However, few of them take into consideration the potential cluster information contained implicitly in the high-dimensional data. In this paper, we propose LaptSNE, a new graph-layout nonlinear dimensionality reduction method based on t-SNE, one of the best techniques for visualizing high-dimensional data as 2D scatter plots. Specifically, LaptSNE leverages the eigenvalue information of the graph Laplacian to shrink the potential clusters in the low-dimensional embedding when learning to preserve the local and global structure from high-dimensional space to low-dimensional space. It is nontrivial to solve the proposed model because the eigenvalues of normalized symmetric Laplacian are functions of the decision variable. We provide a majorization-minimization algorithm with convergence guarantee to solve the optimization problem of LaptSNE and show how to calculate the gradient analytically, which may be of broad interest when considering optimization with Laplacian-composited objective. We evaluate our method by a formal comparison with state-of-the-art methods, both visually and via established quantitative measurements. The results demonstrate the superiority of our method over baselines such as t-SNE and UMAP. We also extend our method to spectral clustering and establish an accurate and parameter-free clustering algorithm, which provides us high reliability and convenience in real applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge