$L_p$-Norm Constrained Coding With Frank-Wolfe Network

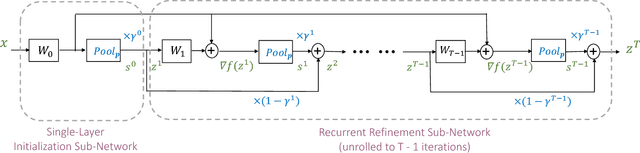
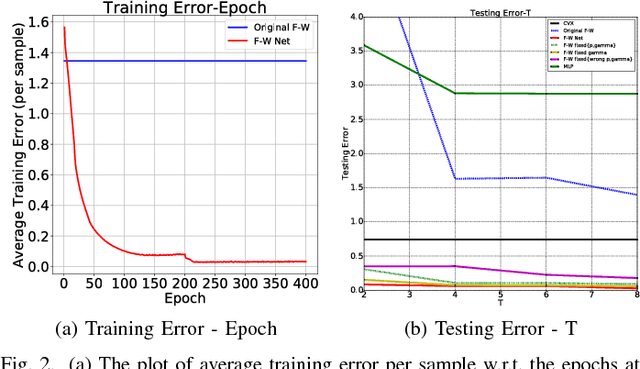
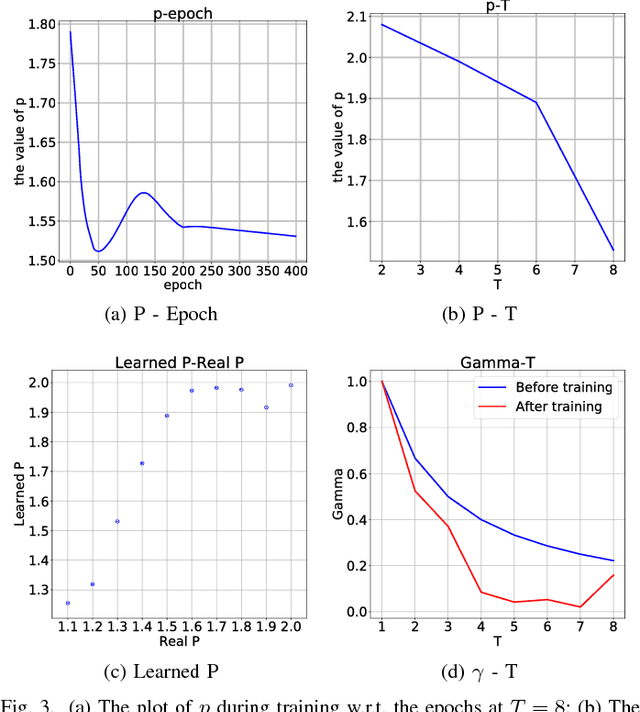
We investigate the problem of $L_p$-norm constrained coding, i.e. converting signal into code that lies inside an $L_p$-ball and most faithfully reconstructs the signal. While previous works known as sparse coding have addressed the cases of $L_0$ and $L_1$ norms, more general cases with other $p$ values, especially with unknown $p$, remain a difficulty. We propose the Frank-Wolfe Network (F-W Net), whose architecture is inspired by unrolling and truncating the Frank-Wolfe algorithm for solving an $L_p$-norm constrained problem. We show that the Frank-Wolfe solver for the $L_p$-norm constraint leads to a novel closed-form nonlinear unit, which is parameterized by $p$ and termed $pool_p$. The $pool_p$ unit links the conventional pooling, activation, and normalization operations, making F-W Net distinct from existing deep networks either heuristically designed or converted from projected gradient descent algorithms. We further show that the hyper-parameter $p$ can be made learnable instead of pre-chosen in F-W Net, which gracefully solves the $L_p$-norm constrained coding problem with unknown $p$. We evaluate the performance of F-W Net on an extensive range of simulations as well as the task of handwritten digit recognition, where F-W Net exhibits strong learning capability. We then propose a convolutional version of F-W Net, and apply the convolutional F-W Net into image denoising and super-resolution tasks, where F-W Net all demonstrates impressive effectiveness, flexibility, and robustness.