KNH: Multi-View Modeling with K-Nearest Hyperplanes Graph for Misinformation Detection
Paper and Code
Feb 15, 2021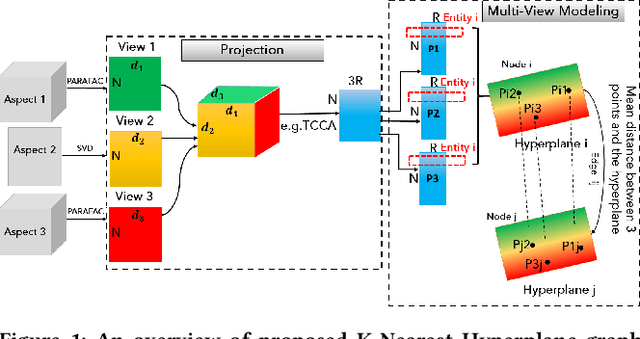

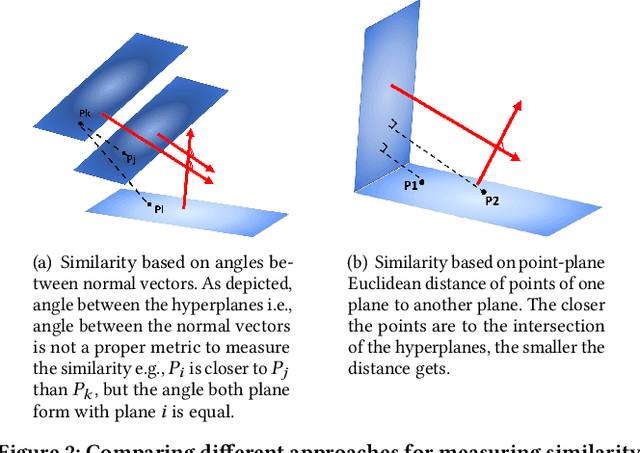
Graphs are one of the most efficacious structures for representing datapoints and their relations, and they have been largely exploited for different applications. Previously, the higher-order relations between the nodes have been modeled by a generalization of graphs known as hypergraphs. In hypergraphs, the edges are defined by a set of nodes i.e., hyperedges to demonstrate the higher order relationships between the data. However, there is no explicit higher-order generalization for nodes themselves. In this work, we introduce a novel generalization of graphs i.e., K-Nearest Hyperplanes graph (KNH) where the nodes are defined by higher order Euclidean subspaces for multi-view modeling of the nodes. In fact, in KNH, nodes are hyperplanes or more precisely m-flats instead of datapoints. We experimentally evaluate the KNH graph on two multi-aspect datasets for misinformation detection. The experimental results suggest that multi-view modeling of articles using KNH graph outperforms the classic KNN graph in terms of classification performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge