Kernelized Classification in Deep Networks

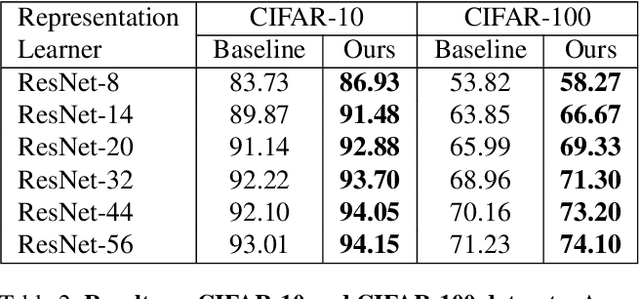
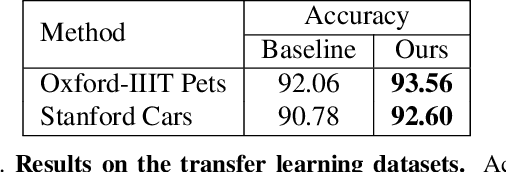
In this paper, we propose a kernelized classification layer for deep networks. Although conventional deep networks introduce an abundance of nonlinearity for representation (feature) learning, they almost universally use a linear classifier on the learned feature vectors. We introduce a nonlinear classification layer by using the kernel trick on the softmax cross-entropy loss function during training and the scorer function during testing. Furthermore, we study the choice of kernel functions one could use with this framework and show that the optimal kernel function for a given problem can be learned automatically within the deep network itself using the usual backpropagation and gradient descent methods. To this end, we exploit a classic mathematical result on the positive definite kernels on the unit n-sphere embedded in the (n+1)-dimensional Euclidean space. We show the usefulness of the proposed nonlinear classification layer on several vision datasets and tasks.