Kernel-based Inference of Functions over Graphs
Paper and Code
Apr 10, 2018
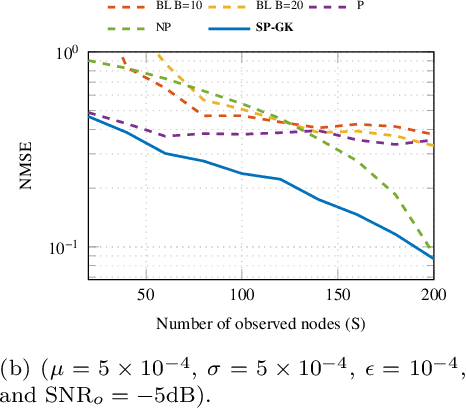
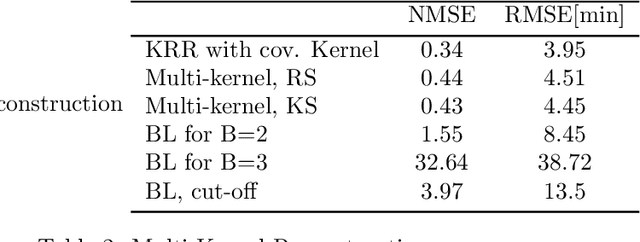
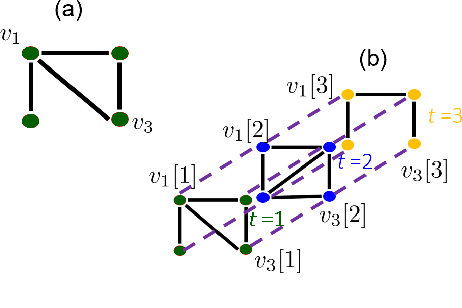
The study of networks has witnessed an explosive growth over the past decades with several ground-breaking methods introduced. A particularly interesting -- and prevalent in several fields of study -- problem is that of inferring a function defined over the nodes of a network. This work presents a versatile kernel-based framework for tackling this inference problem that naturally subsumes and generalizes the reconstruction approaches put forth recently by the signal processing on graphs community. Both the static and the dynamic settings are considered along with effective modeling approaches for addressing real-world problems. The herein analytical discussion is complemented by a set of numerical examples, which showcase the effectiveness of the presented techniques, as well as their merits related to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge