Kernel Bandwidth Selection for SVDD: Peak Criterion Approach for Large Data
Paper and Code
May 19, 2017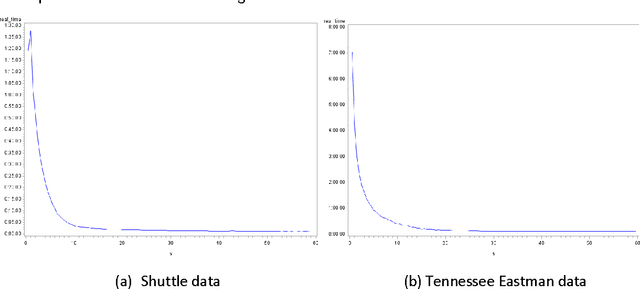

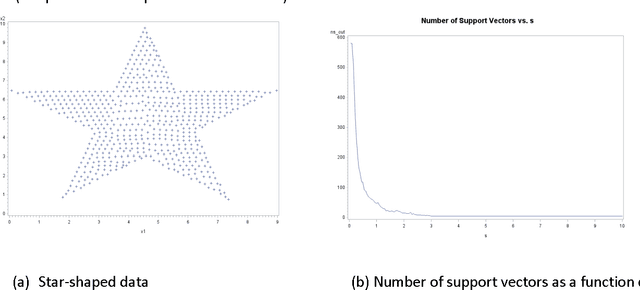
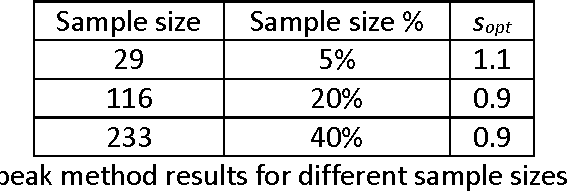
Support Vector Data Description (SVDD) provides a useful approach to construct a description of multivariate data for single-class classification and outlier detection with various practical applications. Gaussian kernel used in SVDD formulation allows flexible data description defined by observations designated as support vectors. The data boundary of such description is non-spherical and conforms to the geometric features of the data. By varying the Gaussian kernel bandwidth parameter, the SVDD-generated boundary can be made either smoother (more spherical) or tighter/jagged. The former case may lead to under-fitting, whereas the latter may result in overfitting. Peak criterion has been proposed to select an optimal value of the kernel bandwidth to strike the balance between the data boundary smoothness and its ability to capture the general geometric shape of the data. Peak criterion involves training SVDD at various values of the kernel bandwidth parameter. When training datasets are large, the time required to obtain the optimal value of the Gaussian kernel bandwidth parameter according to Peak method can become prohibitively large. This paper proposes an extension of Peak method for the case of large data. The proposed method gives good results when applied to several datasets. Two existing alternative methods of computing the Gaussian kernel bandwidth parameter (Coefficient of Variation and Distance to the Farthest Neighbor) were modified to allow comparison with the proposed method on convergence. Empirical comparison demonstrates the advantage of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge