KERMIT: Generative Insertion-Based Modeling for Sequences
Paper and Code
Jun 04, 2019

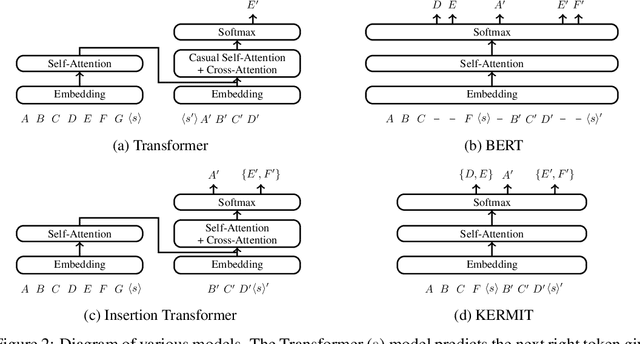
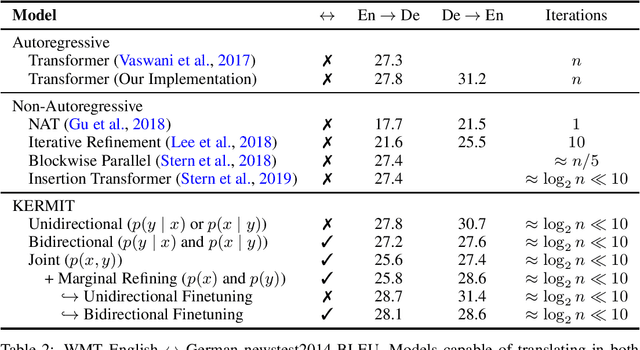
We present KERMIT, a simple insertion-based approach to generative modeling for sequences and sequence pairs. KERMIT models the joint distribution and its decompositions (i.e., marginals and conditionals) using a single neural network and, unlike much prior work, does not rely on a prespecified factorization of the data distribution. During training, one can feed KERMIT paired data $(x, y)$ to learn the joint distribution $p(x, y)$, and optionally mix in unpaired data $x$ or $y$ to refine the marginals $p(x)$ or $p(y)$. During inference, we have access to the conditionals $p(x \mid y)$ and $p(y \mid x)$ in both directions. We can also sample from the joint distribution or the marginals. The model supports both serial fully autoregressive decoding and parallel partially autoregressive decoding, with the latter exhibiting an empirically logarithmic runtime. We demonstrate through experiments in machine translation, representation learning, and zero-shot cloze question answering that our unified approach is capable of matching or exceeding the performance of dedicated state-of-the-art systems across a wide range of tasks without the need for problem-specific architectural adaptation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge