KALE: When Energy-Based Learning Meets Adversarial Training

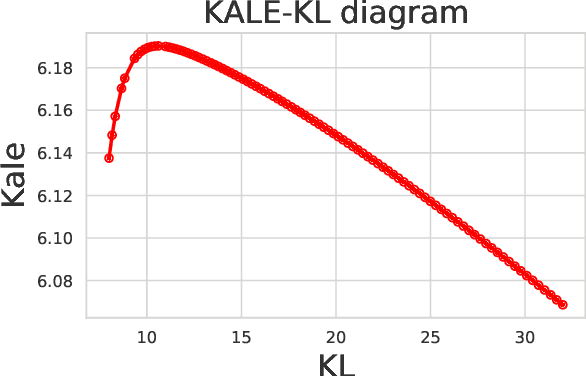
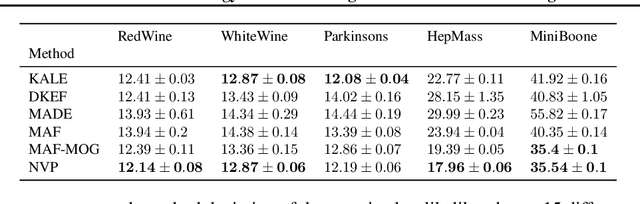
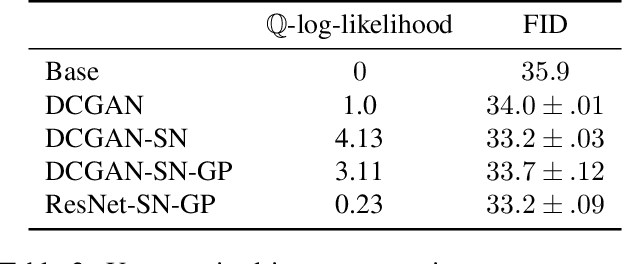
Legendre duality provides a variational lower-bound for the Kullback-Leibler divergence (KL) which can be estimated using samples, without explicit knowledge of the density ratio. We use this estimator, the \textit{KL Approximate Lower-bound Estimate} (KALE), in a contrastive setting for learning energy-based models, and show that it provides a maximum likelihood estimate (MLE). We then extend this procedure to adversarial training, where the discriminator represents the energy and the generator is the base measure of the energy-based model. Unlike in standard generative adversarial networks (GANs), the learned model makes use of both generator and discriminator to generate samples. This is achieved using Hamiltonian Monte Carlo in the latent space of the generator, using information from the discriminator, to find regions in that space that produce better quality samples. We also show that, unlike the KL, KALE enjoys smoothness properties that make it suitable for adversarial training, and provide convergence rates for KALE when the negative log density ratio belongs to the variational family. Finally, we demonstrate the effectiveness of this approach on simple datasets.