k-sums: another side of k-means
Paper and Code
May 19, 2020
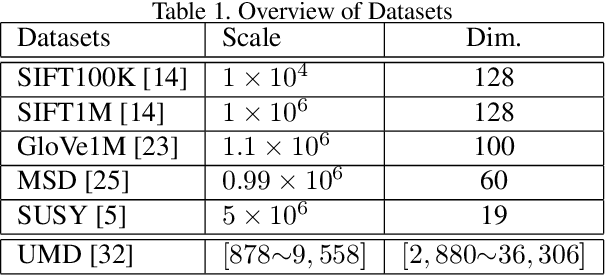


In this paper, the decades-old clustering method k-means is revisited. The original distortion minimization model of k-means is addressed by a pure stochastic minimization procedure. In each step of the iteration, one sample is tentatively reallocated from one cluster to another. It is moved to another cluster as long as the reallocation allows the sample to be closer to the new centroid. This optimization procedure converges faster to a better local minimum over k-means and many of its variants. This fundamental modification over the k-means loop leads to the redefinition of a family of k-means variants. Moreover, a new target function that minimizes the summation of pairwise distances within clusters is presented. We show that it could be solved under the same stochastic optimization procedure. This minimization procedure built upon two minimization models outperforms k-means and its variants considerably with different settings and on different datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge