Joint State and Input Estimation of Agent Based on Recursive Kalman Filter Given Prior Knowledge

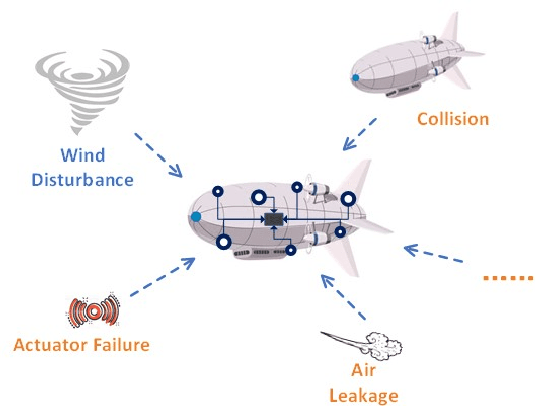
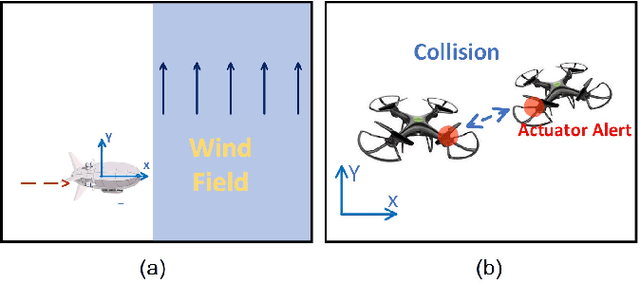
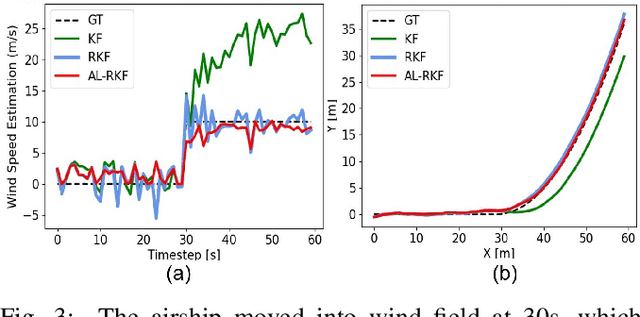
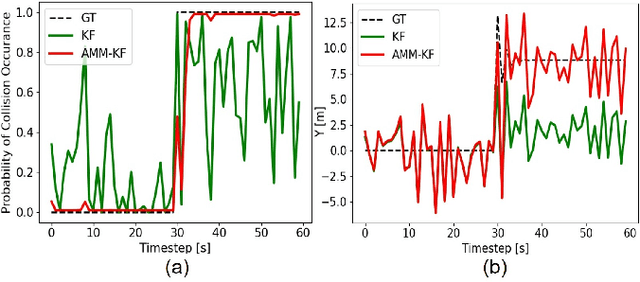
Modern autonomous systems are purposed for many challenging scenarios, where agents will face unexpected events and complicated tasks. The presence of disturbance noise with control command and unknown inputs can negatively impact robot performance. Previous research of joint input and state estimation separately study the continuous and discrete cases without any prior information. This paper combines the continuous space and discrete space estimation into a unified theory based on the Expectation-Maximum (EM) algorithm. By introducing prior knowledge of events as the constraint, inequality optimization problems are formulated to determine a gain matrix or dynamic weights to realize an optimal input estimation with lower variance and more accurate decision-making. Finally, statistical results from experiments show that our algorithm owns 81\% improvement of the variance than KF and 47\% improvement than RKF in continuous space; a remarkable improvement of right decision-making probability of our input estimator in discrete space, identification ability is also analyzed by experiments.