Joint inference and input optimization in equilibrium networks
Paper and Code
Nov 25, 2021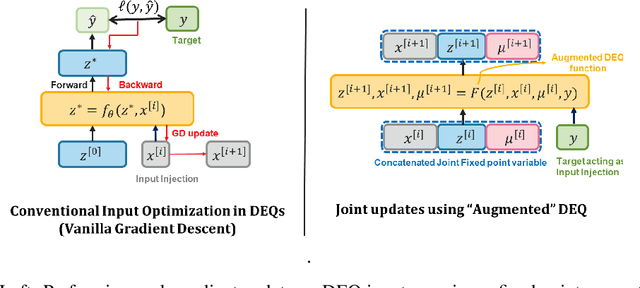
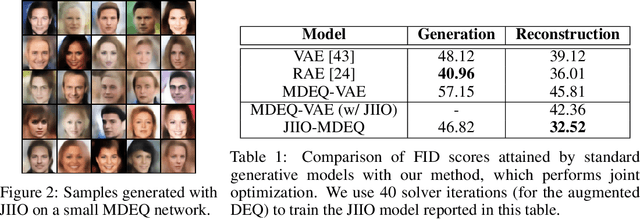
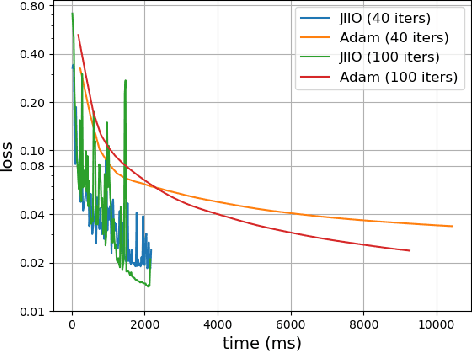

Many tasks in deep learning involve optimizing over the \emph{inputs} to a network to minimize or maximize some objective; examples include optimization over latent spaces in a generative model to match a target image, or adversarially perturbing an input to worsen classifier performance. Performing such optimization, however, is traditionally quite costly, as it involves a complete forward and backward pass through the network for each gradient step. In a separate line of work, a recent thread of research has developed the deep equilibrium (DEQ) model, a class of models that foregoes traditional network depth and instead computes the output of a network by finding the fixed point of a single nonlinear layer. In this paper, we show that there is a natural synergy between these two settings. Although, naively using DEQs for these optimization problems is expensive (owing to the time needed to compute a fixed point for each gradient step), we can leverage the fact that gradient-based optimization can \emph{itself} be cast as a fixed point iteration to substantially improve the overall speed. That is, we \emph{simultaneously} both solve for the DEQ fixed point \emph{and} optimize over network inputs, all within a single ``augmented'' DEQ model that jointly encodes both the original network and the optimization process. Indeed, the procedure is fast enough that it allows us to efficiently \emph{train} DEQ models for tasks traditionally relying on an ``inner'' optimization loop. We demonstrate this strategy on various tasks such as training generative models while optimizing over latent codes, training models for inverse problems like denoising and inpainting, adversarial training and gradient based meta-learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge