Itô-Taylor Sampling Scheme for Denoising Diffusion Probabilistic Models using Ideal Derivatives
Paper and Code
Dec 26, 2021


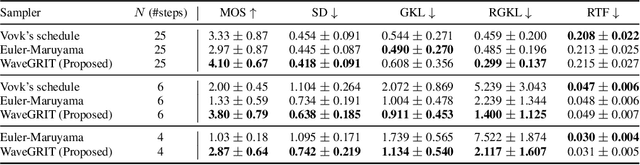
Denoising Diffusion Probabilistic Models (DDPMs) have been attracting attention recently as a new challenger to popular deep neural generative models including GAN, VAE, etc. However, DDPMs have a disadvantage that they often require a huge number of refinement steps during the synthesis. To address this problem, this paper proposes a new DDPM sampler based on a second-order numerical scheme for stochastic differential equations (SDEs), while the conventional sampler is based on a first-order numerical scheme. In general, it is not easy to compute the derivatives that are required in higher-order numerical schemes. However, in the case of DDPM, this difficulty is alleviated by the trick which the authors call "ideal derivative substitution". The newly derived higher-order sampler was applied to both image and speech generation tasks, and it is experimentally observed that the proposed sampler could synthesize plausible images and audio signals in relatively smaller number of refinement steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge