Investigating the locality of neural network training dynamics
Paper and Code
Nov 01, 2021
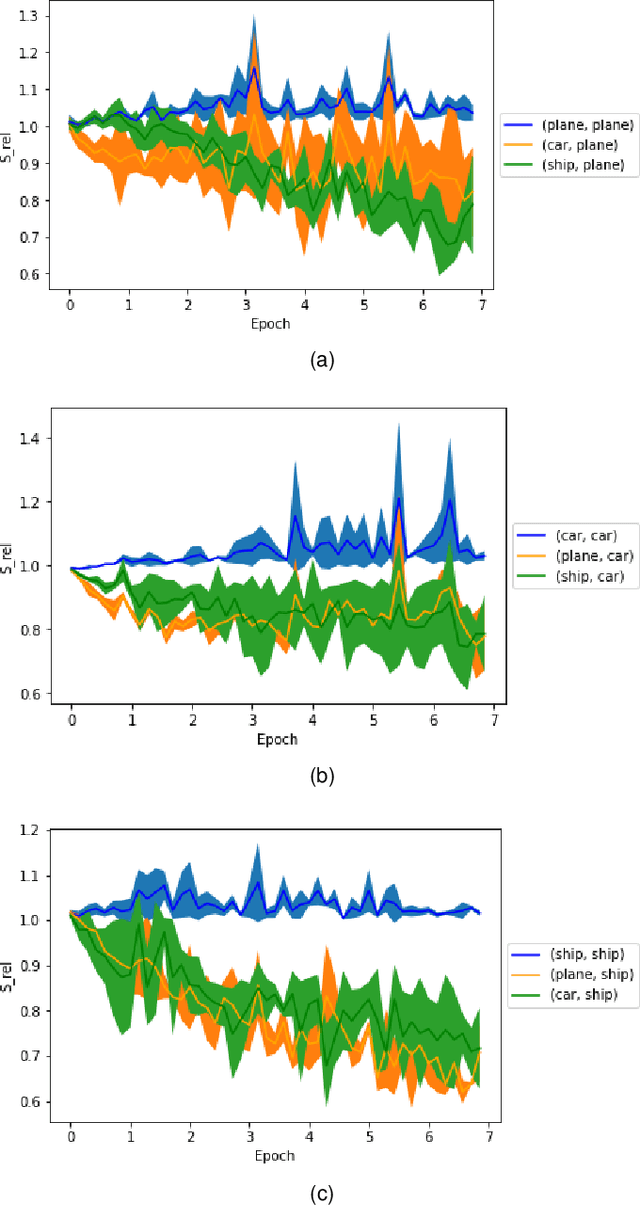
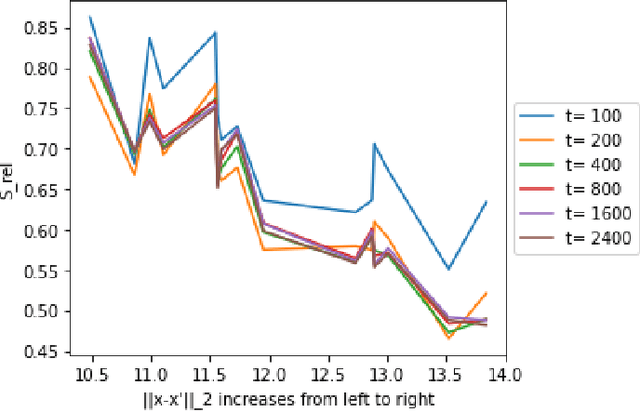
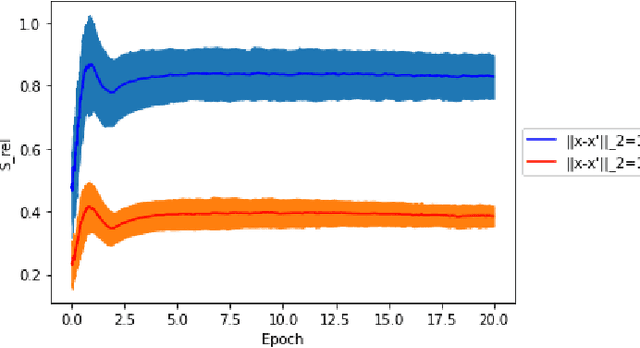
A fundamental quest in the theory of deep-learning is to understand the properties of the trajectories in the weight space that a learning algorithm takes. One such property that had very recently been isolated is that of "local elasticity" ($S_{\rm rel}$), which quantifies the propagation of influence of a sampled data point on the prediction at another data point. In this work, we perform a comprehensive study of local elasticity by providing new theoretical insights and more careful empirical evidence of this property in a variety of settings. Firstly, specific to the classification setting, we suggest a new definition of the original idea of $S_{\rm rel}$. Via experiments on state-of-the-art neural networks training on SVHN, CIFAR-10 and CIFAR-100 we demonstrate how our new $S_{\rm rel}$ detects the property of the weight updates preferring to make changes in predictions within the same class of the sampled data. Next, we demonstrate via examples of neural nets doing regression that the original $S_{\rm rel}$ reveals a $2-$phase behaviour: that their training proceeds via an initial elastic phase when $S_{\rm rel}$ changes rapidly and an eventual inelastic phase when $S_{\rm rel}$ remains large. Lastly, we give multiple examples of learning via gradient flows for which one can get a closed-form expression of the original $S_{\rm rel}$ function. By studying the plots of these derived formulas we given a theoretical demonstration of some of the experimentally detected properties of $S_{\rm rel}$ in the regression setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge